网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
下列多项式为正定二次型的是()。

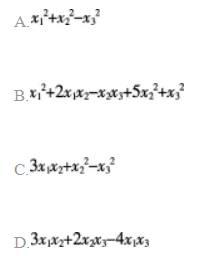
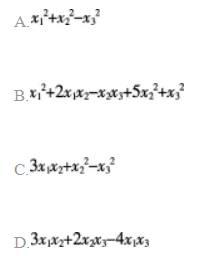
参考答案

参考解析
解析：二次型正定的充要条件是它对应的矩阵的顺序主子式全大于零。对四个选项的二次型所对应的矩阵逐一验证即可。下面只给出B选项中二次型的验证过程。
更多 “下列多项式为正定二次型的是()。 ” 相关考题
考题 二次型为正定的充要条件是对应的矩阵为正定矩阵。() 此题为判断题(对，错)。
查看答案
考题 已知多项式P(x),过点(0,0)(2,8)(4,64)(11,1331)(15,3375),它的三阶差商为常数1,一阶二阶差商均不是0,那么P(x)是() A、二次多项式B、不超过二次的多项式C、三次多项式D、四次多项式
查看答案
考题 下列说法正确的是().A.任一个二次型的标准形是唯一的 B.若两个二次型的标准形相同,则两个二次型对应的矩阵的特征值相同 C.若一个二次型的标准形系数中没有负数,则该二次型为正定二次型 D.二次型的标准形不唯一,但规范形是唯一的
查看答案
考题 实二次型矩阵A正定的充分必要条件是（ ）。A.二次型的标准形的n个系数全为正 B.|A|＞0 C.矩阵A的特征值为2 D.r（A）=n
查看答案
考题 下列二次型中正定二次型是（ ）。
查看答案
考题 要使得二次型为正定的，则t的取值条件是： A. -1 B. -1 C. t>0 D. t
查看答案
考题 二次型当满足（）时，是正定二次型。 A.λ>0 B.λ>-1 C.λ>1 D.以上选项均不成立
查看答案
考题 判别下列二次型的正定性
查看答案
考题 t满足什么条件时，下列二次型是正定的(1) (2)
查看答案
考题 若二次型是正定的，则t的取值范围是_______，
查看答案
考题 设U为可逆矩阵, , 证明为正定二次型
查看答案
考题 设为正定二次型, 求a.
查看答案
考题 判断二次型的正定性
查看答案
考题 以下多项式是二次型（ ）。
查看答案
考题 二次型x2-3xy+y2是( )。A.正定的 B.半正定的 C.负定的 D.半负定的
查看答案
考题 下列多项式为二次型的是()。
查看答案
考题 二次型x2-xy+y2是( )。A.正定的 B.半正定的 C.负定的 D.半负定的
查看答案
考题 若矩阵A的所有奇数阶主子式小于零，而所有偶数阶主子式大于零，则该矩阵为（）矩阵。A、正定B、正定二次型C、负定D、负定二次型
查看答案
考题 若矩阵A的各阶顺序主子式均大于零，则该矩阵为（）矩阵。A、正定B、正定二次型C、负定D、负定二次型
查看答案
考题 要使得二次型为正定的，则t的取值条件是（）。A、-1B、-1C、t0D、t-1
查看答案
考题 二次型，当满足（）时，是正定二次型。A、λ-1B、λ0C、λ1D、λ≥1
查看答案
考题 已知是正定二次型，则（）．A、t0B、t0
查看答案
考题 实数域上的不可约多项式有哪些？（）A、只有一次多项式B、只有判别式小于0的二次多项式C、只有一次多项式和判别式小于0的二次多项式D、任意多项式
查看答案
考题 单选题要使得二次型为正定的，则t的取值条件是（）。A -1B -1C t0D t-1
查看答案
考题 单选题二次型，当满足（）时，是正定二次型。A λ-1B λ0C λ1D λ≥1
查看答案
考题 单选题若矩阵A的所有奇数阶主子式小于零，而所有偶数阶主子式大于零，则该矩阵为（）矩阵。A 正定B 正定二次型C 负定D 负定二次型
查看答案
考题 单选题若矩阵A的各阶顺序主子式均大于零，则该矩阵为（）矩阵。A 正定B 正定二次型C 负定D 负定二次型
查看答案
热门标签
最新试卷