网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设a、b为实数,0
参考答案
参考解析
解析:证明:令集合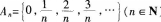 取n足够大使得
取n足够大使得 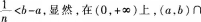
 又A。中的数字都是有理数,...(n,b)中肯定有有理数,证毕。
又A。中的数字都是有理数,...(n,b)中肯定有有理数,证毕。
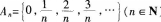 取n足够大使得
取n足够大使得 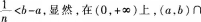
 又A。中的数字都是有理数,...(n,b)中肯定有有理数,证毕。
又A。中的数字都是有理数,...(n,b)中肯定有有理数,证毕。
更多 “设a、b为实数,0” 相关考题
考题
若a,b,C为实数,且a≠o.设甲:b2-4ac≥0,乙:ax2+bx+C-0有实数根, 则 ( )A.甲既不是乙的充分条件,也不是乙的必要条件B.甲是乙的必要条件,但不是乙的充分条件C.甲是乙的充分必要条件D.甲是乙的充分条件,但不是乙的必要条件
考题
正态分布计算所依据的重要性质为( )。A.设X~N(μ,σ2),则u=(X-μ)/σ~N(0,1)B.设X~N(μ,σ2),则对任意实数a、b有P(X<b)=Ф[(b-μ)/σ)C.设X~N(μ,σ2),则对任意实数a、b有P(X>a)=1-Ф[(a-μ)/σ]D.设X~N(μ,σ2),则对任意实数a、b有P(a<X<b)=Ф[(b-μ)/σ)-Ф[(a-μ)/σ]E.设X~μ(μ1,,Y~N(μ2,,则X+Y~N(μ1+μ2,(σ1+σ2) 2)
考题
设随机变量X~N(0,σ2),则对于任何实数λ,都有:
A. P(X≤λ)=P(X≥λ)
B.P(X≥λ)=P(X≤-λ)
C.X-λ~N(λ,σ2-λ2)
D.λX~N(0,λσ2)
考题
设随机变量X?N(0,σ2),则对于任何实数λ都有:
(A) P(X≤λ)=P(X≥λ)(B)P(X≥λ)= P(X≤-λ)
(C) X-λ~N(λ,σ2-λ2)(D)λX~N(0,λσ2)
考题
已知二次函数f(x)的二次项系数为实数a,且其图像与直线2x+y=0交点横坐标为1和3.
(1)若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数n的取值范围.
考题
正态分布计算所依据的重要性质为( )。
A.设X~N(μ,σ2),则μ= (X-μ)/σ~N(0, 1)
B.设X~N(μ,σ2),则对任意实数a、b有P(XC.设X~N(μ,σ2),则对任意实数a、b有P(X>a) =1-Φ[(a-μ)/σ]
D.设X~N(μ,σ2),则对任意实数a、b有P(a
考题
设总体X的分布函数为
其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.
(Ⅰ)求EX与EX^2;
(Ⅱ)求θ的最大似然估计量.
(Ⅲ)是否存在实数a,使得对任何ε>0,都有?
考题
设M为3×3实数矩阵,a为M的实特征值λ的特征向量,则下列叙述正确的是( )。
A、当λ≠0时,Ma垂直于a
B、当λ>0时,Ma与a方向相反
C、当λ<0时,Ma与a方向相反
D、向量Ma与a共线
考题
点(0,1)是曲线y=ax3+bx2+c的拐点,则有()A、a=1,b=-3,c=1B、a为不等于0的任意实数,b=0,c=1C、a=1,b=0,c为不等于1的任意实数D、a、b为任意值,c为不等于1的任意实数
考题
点(0,1)是曲线y=ax3+bx+c的拐点,则a、b、c的值分别为()A、a=1,b=-3,c=-2B、a≠0的实数,b为任意实数,c=1C、a=1,b=0,c=2D、a=0、b为任意实数,c=1
考题
单选题点(0,1)是曲线y=ax3+bx2+c的拐点,则有()A
a=1,b=-3,c=1B
a为不等于0的任意实数,b=0,c=1C
a=1,b=0,c为不等于1的任意实数D
a、b为任意值,c为不等于1的任意实数
考题
问答题设f(x)在[a,b]上连续,在(a,b)内可导,且f(a)·f(b)>0,f(a)·f[(a+b)/2]<0。试证:对任意实数k,∃ξ∈(a,b),使得f′(ξ)=kf(ξ)。
考题
单选题已知以x为未知数的方程x2-(k+1)x+k=0,那么( ).A
对于任何实数k,方程都没有实数根B
对于任何实数k,方程都有实数根C
对于某些实数k,方程有实数根;对于其他实数k,方程没有实数根D
方程是否有实数根无法确定
考题
单选题点(0,1)是曲线y=ax3+bx+c的拐点,则a、b、c的值分别为:()A
a=1,b=-3,c=2B
Ba≠0的实数,b为任意实数,c=1C
a=1,b=0,c=2D
a=0,b为任意实数,c=1
热门标签
最新试卷