网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
已知变换矩阵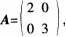
则A将空间曲面(x一1)2+(y一2)2=-4变成( )。
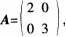则A将空间曲面(x一1)2+(y一2)2=-4变成( )。A、圆
B、椭圆
C、抛物线
D、双曲线
B、椭圆
C、抛物线
D、双曲线
参考答案
参考解析
解析：设曲面经矩阵A变化后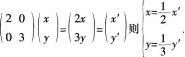为
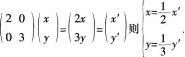故其方程为
故其方程为
更多 “已知变换矩阵则A将空间曲面(x一1)2+(y一2)2=-4变成( )。A、圆 B、椭圆 C、抛物线 D、双曲线 ” 相关考题
考题
设X1,X2,X3,X4,X5为来自正态总体X～N(0,4)的简单随机样本,y=a（X1-2X2）^2+b(3X3-4X3)^2+(abc≠o),且y～χ^2（n）,则a=_______,b=_______,c=_______,b=_______.
考题
过点A(1,-1)，B(-1,1)且圆心在直线x+y-2=0上的圆的方程是（ ）。
A.(x-3)2+(y+1)2=4
B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4
D.(x+1)2+(y+1)2=4
考题
已知曲面方程为x-yZ+z2-2x+8y+6z=10，则过点(5，-2.1)的切平面方程为( )。
A、2x+3y+2z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0
考题
将平面曲线y=x2分别绕y轴和x轴旋转一周，所得旋转曲面分别记作S1和S2。
(1)在空间直角坐标系中，分别写出曲面S1和S2的方程；
(2)求平面y=4与曲面S1。所围成的立体的体积。
考题
将双曲线C://绕x轴旋转一周所生成的旋转曲面的方程是（）．A、4（x2+z2）-9y2=36B、4x2-9（y2+z2）=36C、4x2-9y2=36D、4（x2+y2）-9z2=36
考题
单选题设平面α平行于两直线x/2＝y/（－2）＝z及2x＝y＝z，且与曲面z＝x2＋y2＋1相切，则α的方程为（ ）。A
4x＋2y－z＝0B
4x－2y＋z＋3＝0C
16x＋8y－16z＋11＝0D
16x－8y＋8z－1＝0
考题
单选题设α(→)1，α(→)2，α(→)3，α(→)4是4维非零列向量组，A＝（α(→)1，α(→)2，α(→)3，α(→)4），A*是A的伴随矩阵，已知方程组AX(→)＝0(→)的基础解系为k（1，0，2，0）T，则方程组A*X(→)＝0(→)的基础解系为（ ）。A
α(→)1，α(→)2，α(→)3B
α(→)1＋α(→)2，α(→)2＋α(→)3，3α(→)3C
α(→)2，α(→)3，α(→)4D
α(→)1＋α(→)2，α(→)2＋α(→)3，α(→)3＋α(→)4，α(→)4＋α(→)1
考题
单选题已知曲面x2+2y2+3z2=21上点P与平面x+4y+6z=1的距离最近，则点P的坐标是：（）A
（1，2，-2）B
（1，2，2）C
（-1，-2，2）D
（-1，-2，-2）
考题
单选题设函数φ（x）具有二阶连续导数且φ（0）＝0，并且已知yφ（x）dx＋[sinx－φ（x）]dy＝0是一个全微分方程，则φ（x）＝（ ）。A
－e－x/2＋（cosx）/2＋（sinx）/2B
x3－x2/2＋1C
x2ex－2D
（xcosx）/2＋C1cosx＋C2sinx
考题
单选题已知A为3×4矩阵，X(→)＝（x1，x2，x3，x4）T，AX(→)＝0(→)有通解k（1，l，0，－1）T，其中k为任意常数，将A中去掉第i列（i＝1，2，3，4）的矩阵记为Ai，则下列方程组中有非零解的是（ ）。A
A1Y(→)＝0(→)B
A2Y(→)＝0(→)C
A3Y(→)＝0(→)D
A4Y(→)＝0(→)
考题
单选题已知曲面z＝4－x2－y2上点P处的切平面平行于平面π：2x＋2y＋z－1＝0，则点P的坐标是（ ）。A
（1，－1，2）B
（－1，1，2）C
（1，1，2）D
（－1，－1，2）
热门标签
最新试卷