网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
将平面曲线y=x2分别绕y轴和x轴旋转一周,所得旋转曲面分别记作S1和S2。
(1)在空间直角坐标系中,分别写出曲面S1和S2的方程;
(2)求平面y=4与曲面S1。所围成的立体的体积。
(1)在空间直角坐标系中,分别写出曲面S1和S2的方程;
(2)求平面y=4与曲面S1。所围成的立体的体积。
参考答案
参考解析
解析:(1)在空间直角坐标系中,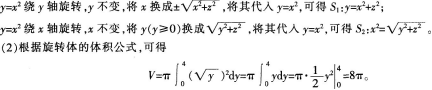
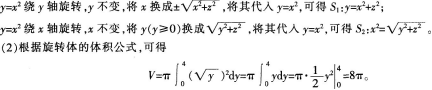
更多 “将平面曲线y=x2分别绕y轴和x轴旋转一周,所得旋转曲面分别记作S1和S2。 (1)在空间直角坐标系中,分别写出曲面S1和S2的方程; (2)求平面y=4与曲面S1。所围成的立体的体积。” 相关考题
考题
设曲线y=f(x)上任一点(x,y)处的切线斜率为(y/x)+x2,且该曲线经过点(1,1/2)。(1)求函数y=f(x);(2)求由曲线y= f(x),y=O,x=1所围图形绕x轴旋转一周所得旋转体的体积V。
考题
旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得?
A. xOy平面上的双曲线绕x轴旋转所得
B. xOz平面上的双曲线绕z轴旋转所得
C. xOy平面上的橢圆绕x轴旋转所得
D. xOz平面上的椭圆绕x轴旋转所得
考题
(1)求直线y=1,曲线L以及y轴围成的平面图形绕y轴旋转一周所得到的的旋转体体积A;(2)假定曲线L绕y轴旋转一周所得到的旋转曲面为S。该旋转曲面作为容器盛满水(水的质量密度(单位体积水的重力)等于1),如果将其中的水抽完,求外力作功W.
考题
基本定位件定位套能消除两个不定度,分别是()A、沿X轴方向和沿Y轴方向的移动B、绕X轴方向和绕Y轴方向的转动C、沿X轴方向的移动和绕Y轴方向的转动D、绕X轴方向的转动和沿Y轴方向的移动
考题
旋转曲面x2-y2-z2=1是下列哪个曲线绕何轴旋转所得()?A、xOy平面上的双曲线绕x轴旋转所得B、xOz平面上的双曲线绕z轴旋转所得C、xOy平面上的椭圆绕x轴旋转所得D、xOz平面上的椭圆绕x轴旋转所得
考题
将双曲线C://绕x轴旋转一周所生成的旋转曲面的方程是().A、4(x2+z2)-9y2=36B、4x2-9(y2+z2)=36C、4x2-9y2=36D、4(x2+y2)-9z2=36
考题
单选题方程x2/2+y2/2-z2/3=0表示旋转曲面,它的旋转轴是( )。A
x轴B
y轴C
z轴D
直线x=y=z
热门标签
最新试卷