网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
如图所示,ΔABC是直角三角形,四边形和四边形都是正方形,已知4cm,问正方形HFGF的面积是多少?( )
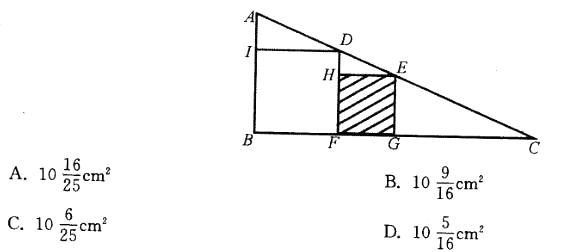

参考答案
参考解析
解析: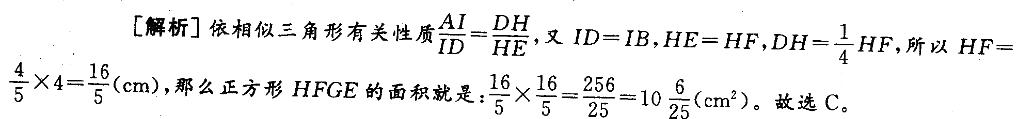
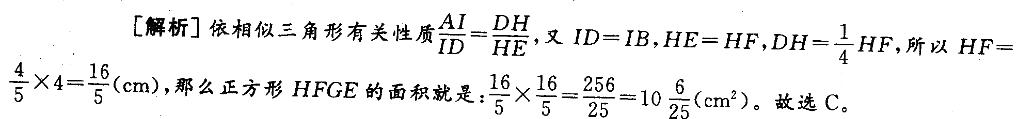
更多 “如图所示,ΔABC是直角三角形,四边形和四边形都是正方形,已知4cm,问正方形HFGF的面积是多少?( ) ” 相关考题
考题
如图,甲、乙、丙、丁四个长方形拼成正方形 EFGH,中间阴影为正方形。已知,甲、乙、丙、丁四个长方形面积的和是 32cm2,四边形 ABCD 的面积是 20cm2。问甲、乙、丙、丁四个长方形周长的总和是( )。(图略)A.32cmB.56cmC.48cmD.68cm
考题
如右图所示,△ABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与△AED的面积之比为3:2,问AE的长度是多少( )
A.6.9 B.7.1 C.7.2 D.7.4
考题
数学运算。在这部分试题中,每道试题呈现一段表述数字关系的文字.要求你迅速、准确地计算出答案。
如图所示,ΔABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与ΔAED的面积之比为3:2。问AE的长度是多少?()
A.6.9
B.7.1
C.7.2
D.7.4
考题
判断题“正方形是平面内每个内角都是直角的四边形。”作为概念是否正确?A
对B
错
热门标签
最新试卷