网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
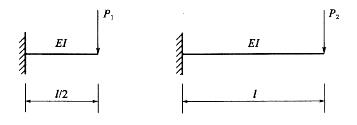
已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2为：

A.2
B. 4
C. 8
D. 16

参考答案

参考解析
解析：
更多 “已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2为： A.2 B. 4 C. 8 D. 16 ” 相关考题
考题 两简支梁，一根为刚，一根为铜，已知它们的抗弯刚度相同。跨中作用有相同的力F，二者的()不同。A支反力B 最大正应力C 最大挠度D最大转角
查看答案
考题 某悬臂梁其刚度为EI，跨度为l，自由端作用有力F。为减小最大挠度，则下列方案中最佳方案是()
查看答案
考题 图示悬臂梁AD和BE的抗弯刚度同为EI=24×10^6N·m²，由杆CD相连接。CD杆的长度l=5m，截面积A=3×10^-4m²，E=200GPa。若FP=50kN，试求悬臂梁AD在D点的挠度。
查看答案
考题 跨度为l的简支梁已知EI，当整个梁承受均布荷载q时，梁中点挠度Wc=-5ql^4/384EI，图示简支梁跨中挠度Wc=()。
查看答案
考题 如图所示一悬臂梁，其抗弯刚度为FI，受两个力P的作用，则利用卡式定理求自由端C的挠度为( )。
查看答案
考题 两根矩形截面悬臂梁，弹性模量均为E，横截面尺寸如图，两梁的载荷均为作用在自由端的集中力偶。已知两梁的最大挠度相同，则集中力偶Me2是Me1的(悬臂梁受自由端集中力偶M作用，自由端挠度为ML2/2EI) A.8倍 B.4倍 C.2倍 D.1倍
查看答案
考题 已知图示两梁的抗弯截面刚度EI相同，若两者自由端的挠度相等，则P1/P2为: A.2 B.4 C.8 D.16
查看答案
考题 已知图示梁抗弯刚度EI为常数，则用叠加法可得跨中点C的挠度为：
查看答案
考题 已知图示梁抗弯刚度EI为常数，则用叠加法可得自由端C点的挠度为：
查看答案
考题 梁的横截面形状如图示，则截面对Z轴的抗弯截面模量WZ为：
查看答案
考题 已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2为： A.2 B. 4 C. 8 D. 16
查看答案
考题 已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2等于： （A）2 (B)4 (C)8 (D)16
查看答案
考题 在图示体系中，集中质量为m，杆长为l，抗弯刚度为EI，杆重不计。该体系自由振动的周期为（　　）。
查看答案
考题 已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：
查看答案
考题 图示组合结构，梁AB的抗弯刚度为EI，二力杆的抗拉刚度都为EA。DG杆的轴力为（　　）。 A、0 B、P，受拉 C、P，受压 D、2P，受拉
查看答案
考题 图示连续梁，EI=常数，已知支承B处梁截面转角为-7Pl2/240EI（逆时针向），则支承C处梁截面转角φC应为：
查看答案
考题 进行简支梁挠度计算时，用梁的最小刚度Bmin代替材料力学公式中的EI。 Bmin值的含义是： A.沿梁长的平均刚度 B.沿梁长挠度最大处截面的刚度 C.沿梁长内最大弯矩处截面的刚度 D.梁跨度中央处截面的刚度
查看答案
考题 图示为刚架在均布荷载作用下的M图，曲线为二次抛物线，横梁的抗弯刚度为2EI，竖柱为EI，支座A处截面转角为：
查看答案
考题 图示梁的抗弯刚度为EI，长度为l，k＝6EI/l3，跨中C截面弯矩为（以下侧受拉为正）（　　）。 A．0 B．ql2/32 C．ql2/48 D．ql2/64
查看答案
考题 图示梁的抗弯刚度为EI，长度为l，欲使梁中点C弯矩为零，则弹性支座刚度k的取值应为（　　）
查看答案
考题 图示结构当水平支杆产生单位位移时（未注的杆件抗弯刚度为EI），B-B截面的弯矩值为（　　）。
查看答案
考题 沿梁跨度方向，截面抗弯刚度是变化的，所以，验算变形时所采用的截面抗弯刚度是指平均的截面抗弯刚度。
查看答案
考题 两矩形截面悬臂梁，截面宽度相同，截面高度之比为2。若两梁材料相同，梁长之比为2，在自由端受相同集中力作用，则其最大挠度之比为1。
查看答案
考题 梁的挠曲线近似微分方程确立了梁的挠度的（）与弯矩、抗弯刚度之间的关系。梁弯曲时，如果梁的抗弯刚度愈大，则梁的曲率愈（），说明梁愈不容易变形。
查看答案
考题 两悬臂梁，其横截面和材料均相同，在梁的自由端作用有大小相等的集中力，但一梁的长度为另一梁的2倍，则长梁自由端的挠度是短梁的（）倍，转角又是短梁的（）倍。
查看答案
考题 进行简支梁挠度计算时，用梁的最小刚度Bmin代替材料力学公式中的EI。Bmin值的含义是：（）A、沿梁长的平均刚度B、沿梁长挠度最大处截面的刚度C、沿梁长内最大弯矩处截面的刚度D、梁跨度中央处截面的刚度
查看答案
考题 判断题在构件挠度计算时，取同一符号区段中最小弯矩处的截面抗弯刚度作为该梁的抗弯刚度，这就是挠度计算中的最小刚度法。A 对B 错
查看答案
热门标签
最新试卷