网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
空间曲线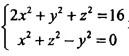 在xOy平面的投影方程是()。
在xOy平面的投影方程是()。
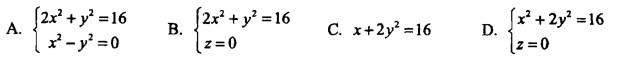
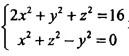 在xOy平面的投影方程是()。
在xOy平面的投影方程是()。
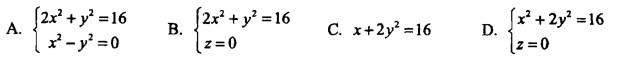
参考答案
参考解析
解析:正确答案是D。
提示:消去z得投影柱面方程X2+2y2=0,再与Z=0联立。
提示:消去z得投影柱面方程X2+2y2=0,再与Z=0联立。
更多 “空间曲线在xOy平面的投影方程是()。 ” 相关考题
考题
球面x2 + y2 + z2 = 9与平面x + z = 1的交线在xoy坐标面上投影的方程是:
(A) x2 + y2 + (1-x)2 = 9
(C) (1-z)2 + y2 + z2 = 9
考题
填空题将物体连同确定其空间位置的直角坐标系,用斜投影的方法投射到与XOY坐标面()的轴测投影面上,所得到的轴测图称为水平斜等轴测图。
热门标签
最新试卷