考题
滇红品种为云南大叶种,其滋味( )。A.浓醇,收敛性强B.浓醇,收敛性弱C.醇和,收敛性强D.醇和,收敛性弱
考题
使用迭代法的关键问题是其收敛性与收敛速度,收敛性与迭代初值的选取有关。()
考题
若级数
在x=-2处收敛,则此级数在x=5处的敛散性是( )。
A.发散
B.条件收敛
C.绝对收敛
D.收敛性不能确定
考题
级数( )。A、发散
B、条件收敛
C、绝对收敛
D、收敛性与α的取值有关
考题
在x=-2处收敛,则此级数在x=5处的敛散性是怎样的?
A.发散 B.条件收敛
C.绝对收敛 D.收敛性不能确定
考题
若级数在x = -2处收敛,则此级数在x= 5处( )。
A.发散 B.条件收敛 C.绝对收敛 D.收敛性不能确定
考题
研究级数的收敛性(即何时绝对收敛,何时条件收敛,何时发散,其中常数a>0.
考题
梯度法与变尺度法所具有的收敛性分别为()A、一次收敛性.一次收敛性B、二次收敛性.二次收敛性C、一次收敛性.二次收敛性D、二次收敛性.一次收敛性
考题
滇红品种为云南大叶种,其滋味()。A、清醇,收敛性强B、清醇,收敛性弱C、浓醇,收敛性强D、浓醇,收敛性弱
考题
用云南大叶种加工的滇红,其滋味()。A、清醇,收敛性强B、清醇,收敛性弱C、浓醇,收敛性强D、浓醇,收敛性弱
考题
最先明确定义无穷级数收敛性的数学家是(),他是()。
考题
()首先给出了微积分无穷级数收敛性的判别法。A、丹尼尔·伯努利B、奥古斯丁·路易·柯西C、雅各布·伯努利D、路易吉·圭多·格兰第
考题
马尔萨斯的人口论中指出人口的增长是呈什么级数增长的?()A、算术级数B、对数级数C、几何级数D、指数级数
考题
关于反应级数的各种说法中正确的是()。A、只有基元反应的级数是正整数B、反应级数不会小于零C、反应总级数一定大于对任一反应物级数D、反应级数都可通过实验来确定
考题
下列命题中,错误的是().A、部分和数列{s}有界是正项级数收敛的充分条件B、若级数绝对收敛,则级数必定收敛C、若级数条件收敛,则级数必定发散D、若,则级数收敛
考题
若在x=-1处收敛,则此级数在x=2处().A、条件收敛B、绝对收敛C、发散D、收敛性不能确定
考题
单选题若级数在x=-2处收敛,则此级数在x=5处()。A
发散B
条件收敛C
绝对收敛D
收敛性不能确定
考题
填空题最先明确定义无穷级数收敛性的数学家是(),他是()。
考题
单选题若级数[v]在x=-2处收敛,则此级数在x=5处的敛散性是怎样的?()A
发散B
条件收敛C
绝对收敛D
收敛性不能确定
考题
填空题最先明确定义无穷级数收敛性的数学家是(),他是法国人。
考题
单选题梯度法与变尺度法所具有的收敛性分别为()A
一次收敛性.一次收敛性B
二次收敛性.二次收敛性C
一次收敛性.二次收敛性D
二次收敛性.一次收敛性
考题
单选题()首先给出了微积分无穷级数收敛性的判别法。A
丹尼尔·伯努利B
奥古斯丁·路易·柯西C
雅各布·伯努利D
路易吉·圭多·格兰第
考题
单选题若在x=-1处收敛,则此级数在x=2处().A
条件收敛B
绝对收敛C
发散D
收敛性不能确定
考题
单选题下列命题中,错误的是().A
部分和数列{s}有界是正项级数收敛的充分条件B
若级数绝对收敛,则级数必定收敛C
若级数条件收敛,则级数必定发散D
若,则级数收敛
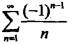 的收敛性是( )。
的收敛性是( )。
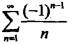 的收敛性是( )。
的收敛性是( )。
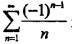 是交错级数,符合莱布尼茨定理条件,收敛,但
是交错级数,符合莱布尼茨定理条件,收敛,但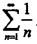 发散,条件收敛,应选B。
发散,条件收敛,应选B。
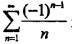 是交错级数,符合莱布尼茨定理条件,收敛,但
是交错级数,符合莱布尼茨定理条件,收敛,但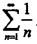 发散,条件收敛,应选B。
发散,条件收敛,应选B。