网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
参数方程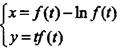 确定了y是x的函数,且f,(t)存在,f(0) = 2, f,(0) = 2,则当t=0时,dy/dx的值等于( )。
确定了y是x的函数,且f,(t)存在,f(0) = 2, f,(0) = 2,则当t=0时,dy/dx的值等于( )。
A. 4/3 B. -4/3 C. -2 D. 2
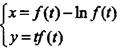 确定了y是x的函数,且f,(t)存在,f(0) = 2, f,(0) = 2,则当t=0时,dy/dx的值等于( )。
确定了y是x的函数,且f,(t)存在,f(0) = 2, f,(0) = 2,则当t=0时,dy/dx的值等于( )。
A. 4/3 B. -4/3 C. -2 D. 2
参考答案
参考解析
解析:正确答案是D。
提示:由参数方程求导公式
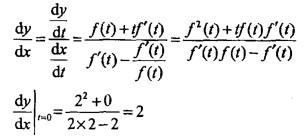
提示:由参数方程求导公式
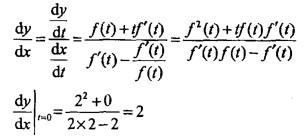
更多 “参数方程确定了y是x的函数,且f,(t)存在,f(0) = 2, f,(0) = 2,则当t=0时,dy/dx的值等于( )。 A. 4/3 B. -4/3 C. -2 D. 2” 相关考题
考题
以下结论正确的是()。
A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
考题
设f(x)是二阶常系数非齐次线性微分方程y″+py′+qy=sin2x+2ex的满足初始条件f(0)=f′(0)=0的特解,则当x→0时,
A.不存在
B.等于0
C.等于1
D.其他
考题
设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)O,f’(x0)=0,则函数f(x)在点x0().A、取得极大值B、取得极小值C、的某个邻域内单调增加D、的某个邻域内单调减少
考题
单选题设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)O,f’(x0)=0,则函数f(x)在点x0().A
取得极大值B
取得极小值C
的某个邻域内单调增加D
的某个邻域内单调减少
考题
单选题设函数f(x)满足关系式f″(x)+[f′(x)]2=x,且f′(0)=0,则( )。A
f(0)是f(x)的极大值B
f(0)是f(x)的极小值C
点(0,f(0))是曲线y=f(x)的拐点D
f(0)不是f(x)的极值,点(0,f(0))也不是曲线y=f(x)的拐点
考题
单选题设函数f(u)可微,且f′(0)=1/2,则z=f(4x2-y2)在点(1,2)处的全微分dz|(1,2)=( )。A
4dx+2dyB
4dx-2dyC
-4dx+2dyD
-4dx-2dy
考题
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。A
f″(x)+f(x)=0B
f′(x)+f(x)=0C
f″(x)+f′(x)=0D
f″(x)+f′(x)+f(x)=0
考题
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A
1/5B
1/7C
-1/7D
-1/5
考题
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A
1B
-1C
1/7D
-1/7
考题
单选题设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。A
f′(x)+f(x)=0B
f′(x)-f(x)=0C
f″(x)+f(x)=0D
f″(x)-f(x)=0
考题
单选题设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=( )。A
-1/2B
-1/4C
-1/7D
-1/9
热门标签
最新试卷