网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
棱长等于1的正方体内接于一球体中,则该球的表面积是( )
A.3π
B.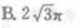
C.6π
D.9π
A.3π
B.
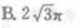
C.6π
D.9π
参考答案
参考解析
解析:

更多 “棱长等于1的正方体内接于一球体中,则该球的表面积是( ) A.3π B. C.6π D.9π” 相关考题
考题
如图1,正方体ABCDA′B′C′D′中,EE′∥FF′∥BB′,平面AEE′A′与平面ABB′A′成15°角,平面AFF′A′与平面ADD′A′成30°角.如果正方体的棱长为1,那么几何体AEF A′E′F′的体积等于____.
考题
一个正方体的边长为1,一只蚂蚁从其一个角出发,沿着正方体的棱形进,直到经过该正方体的每一条棱为止(经过一个顶点即算作经过该顶点所连接的3条棱)。则其最短的行进距离为( )。A. 3
B. 4
C. 5
D. 6
考题
在棱长为1的正方体上切下两个角,所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体,六面体体积为原正方体体积的1/24,则六面体表面积为原正方体表面积的:A.1/4
B.1/6
C.1/8
D.1/10
考题
单选题在棱长为1的正方体上切下两个角,所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体,六面体体积为原正方体体积的1/24,则六面体表面积为原正方体表面积的:A
1/4B
1/6C
1/8D
1/10
热门标签
最新试卷