网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
单层圆柱体内一维径向稳态导热过程中,无内热源,物性参数为常数,则下列说法正确的是( )。
A.导热量Φ为常数
B.导热量Φ为半径的函数
C.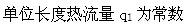
D.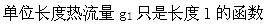
B.导热量Φ为半径的函数
C.
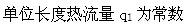
D.
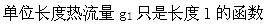
参考答案
参考解析
解析:

更多 “单层圆柱体内一维径向稳态导热过程中,无内热源,物性参数为常数,则下列说法正确的是( )。A.导热量Φ为常数 B.导热量Φ为半径的函数 C. D.” 相关考题
考题
物性参数为常数的一圆柱导线,通过的电流均匀发热,导线与空气间的表面传热系数为定值,建立导线的导热微分方程采用()。
A、柱坐标下一维无内热源的不稳态导热微分热方程B、柱坐标下一维无内热源的稳态导热微分热方程C、柱坐标下一维有内热源的不稳态导热微分热方程D、柱坐标下一维有内热源的稳态导热微分热方程
考题
一维大平壁内稳态无内热源导热过程中,当平壁厚度一定时,不正确的说法是( )。
A. 平壁内温度梯度处处相等
B. 材料导热率大,则壁面两侧温差小
C. 导热率与温度梯度的积为常数
D. 热流量为常数
考题
关于傅里叶准则Fo和毕渥准则Bi,下列说法错误的是( )。A.Fo是非稳态导热过程的无量纲时间
B.Fo反映非稳态导热过程进行的深度
C.Bi是表示物体内部导热热阻与物体表面对流换热热阻的比值
D.Bi>0.1,瞬态导热的加热或冷却问题,可以用集总参数法求解
考题
在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。
A. 温度梯度与热导率成反比
B. 导热过程与材料传导性能无关
C. 热量计算也与热导率无关
D. 边界条件不受物理性质影响
考题
物性参数为常数的一圆柱导线,通过的电流均匀发热,导线与空气间的表面传热系数为定值,建立导线的导热微分方程采用( )。A.柱坐标下一维无内热源的不稳态导热微分方程
B.柱坐标下一维无内热源的稳态导热微分方程
C.柱坐标下一维有内热源的不稳态导热微分方程
D.柱坐标下一维有内热源的稳态导热微分方程
考题
单层圆柱体内径一维径向稳态导热过程中无内热源,物性参数为常数,则下列说法正确的是( )。
A. φ导热量为常数
B. φ为半径的函数
C. q1(热流量)为常数
D. q1只是l的函数
考题
单选题在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。[2018年真题]A
温度梯度与热导率成反比B
导热过程与材料传导性能无关C
热量计算也与热导率无关D
边界条件不受物理性质影响
考题
单选题Biot准则用于某个热物体的对流散热过程求解,()A
Bi越大,说明物体内部的温度分布越均匀,适用集总参数法B
Bi越小,说明物体内部的温度分布越均匀,适用集总参数法C
Bi越大,说明对流比导热占优势,是稳态对流换热过程D
Bi越小,说明导热比对流占优势,是稳态导热过程
考题
单选题一维大平壁内稳态无内热源导热过程中,当平壁厚度一定时,不正确的说法是( )。[2013年真题]A
平壁内温度梯度处处相等B
材料导热率大,则壁面两侧温差小C
导热率与温度梯度的积为常数D
热流量为常数
考题
单选题某一稳态、常物性、无内热源的导热物体的表面最低温度为100℃,那么其内部绝对不可能出现的温度是()A
50℃B
200℃C
1000℃D
2000℃
热门标签
最新试卷