网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
假设厂商的生产函数为
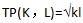
要素K、L价格分别为
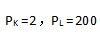
两种要素的投入数量均可以调整。 (1)计算总成本TC(Q)。 (2)若该厂商在产品市场是完全垄断者,且该市场需求曲线是P=2 000-100Q,计算垄断价格。
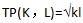
要素K、L价格分别为
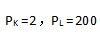
两种要素的投入数量均可以调整。 (1)计算总成本TC(Q)。 (2)若该厂商在产品市场是完全垄断者,且该市场需求曲线是P=2 000-100Q,计算垄断价格。
参考答案
参考解析
解析:

更多 “假设厂商的生产函数为 要素K、L价格分别为 两种要素的投入数量均可以调整。 (1)计算总成本TC(Q)。 (2)若该厂商在产品市场是完全垄断者,且该市场需求曲线是P=2 000-100Q,计算垄断价格。” 相关考题
考题
计算题:假设在完全竞争行业中有许多相同的厂商,代表厂商LAC曲线的最低点的值为6元,产量为500单位;当最优工厂规模为每阶段生产550单位的产品时,各厂商的SAC为7元,还知市场需求函数与供给函数分别是:Qd=8000-5000P,QS=35000+2500P.(1)求市场均衡价格,并判断该行业是长期还是在短期处于均衡?为什么?(2)在长期均衡时,该行业有多少家厂商?(3)如果市场需求函数发生变动,变为Qd1=95000-5000P,试求行业和厂商的新的短期的均衡价格及产量,厂商在新的均衡点上,盈亏状况如何?
考题
假定某厂商的边际成本函数为SMC=3Q2-30Q+100,而且生产10单位产量的总成本为1000, 求:(1)固定成本的值。 (2)总成本函数、总可变成本函数、平均成本函数、平均可变成本函数。
考题
垄断厂商生产某一产品,产品的成本函数为C(q)=q2,市场反需求函数为p=120-q。试求:(1)垄断厂商利润最大化的产量和价格,并画图说明。(2)政府对垄断厂商征收100元的税收后,垄断厂商的产量和价格。(3)政府对垄断厂商单位产品征收从量税2元,垄断厂商的产量和价格。
考题
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。假设该厂商产品的市场需求函数Q=a-0.5P。若劳动力市场是完全竞争的,求该厂商对劳动的需求函数。
考题
假定一个竞争性厂商,其生产函数为Q=f(L,K)=AL^αK^β,生产要素L和K的价格分别为w和r。 (1)试求在K为不变投入时厂商的短期成本函数。 (2)求厂商的长期成本函数,并讨论不同的规模报酬对平均成本曲线形状的影响。
考题
在一个完全竞争市场中,行业的生产成本不变,单个厂商的长期成本函数为LTC=Q3-4002+600Q。又假设该市场的需求函数为Q=13000-5P。问: (1)该行业的长期供给曲线是什么? (2)该行业实现长期均衡时的厂商数量是多少?
考题
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为
消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时候企业个数
考题
已知劳动是唯一的可变要素,生产函数为Q =A +10L - 5L2,产品市场是完全竞争的,劳动价格为W.试说明: (1)厂商为劳动的需求函数。 (2)厂商对劳动的需求量与工资反方向变化。 (3)厂商对劳动的需求量与产品价格同方向变化:
考题
假设有三个厂商,每个厂商的生产计划为:厂商1(-1,3,-6)厂商2(7,-3,-14)厂商3(6,0.5,-20)试证明无论价格(Pi,P2,p3)为多少,厂商1和2的利润都不会比厂商3多。
考题
假设某完全竞争行业有200个相同的企业,企业的短期成本函数为TC =0. 2Q2+Q+15,市场需求函数为Qp= 2475 - 95P,厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q,求: (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。
考题
完全竞争行中某厂商的成本函数为TC=Q3-6Q2+30Q+40试求: (1)假设产品价格为66元,利润最大化时的产量及利润总额。 (2)竞争市场供求发生变化,由此决定的新价格为30元,在新价格下,厂商是否会发生亏损?如果会,最小的亏损额为多少? (3)该厂商在什么情况下会停止生产? (4)厂商的短期供给函数。
考题
假设某厂商的生产函数为厂
则以下说法哪个是正确的?( )
A.该厂商的生产函数呈规模报酬不变
B.成本函数是产出的线性函数
C.如果要素z的价格大于要素y的价格的两倍以上,则只能用要素y进行生产
D.以上说法均不正确
考题
假设某完全竞争行业有500个相同的厂商,每个厂商的短期成本函数为:STC=O. 5Q2+Q+10。 (1)求完全竞争市场的短期供给函数。 (2)假设市场需求函数为QD=4 000-400P,求市场的均衡价格和产量。 (3)假定对每一件产品征收0.9元的税,新的市场均衡价格和产量又为多少?厂商和消费者的税收负担各为多少?
考题
问答题已知某厂商的生产函数为Q=0.5L1/3K2/3;当资本投入量K=50时资本的总价值为500;劳动的价格PL=5。求: (1)劳动的投入函数L=L(Q); (2)总成本函数、平均成本函数和边际成本函数; (3)当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少?
热门标签
最新试卷