网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
华强卫星公司向北京和上海的订户发送电视节目,两地订户群体的需求曲线分别为: Qbj =50-(1/3)Pbj,Qsh =80- (2/3)Psh式中,Q以年千户计,P是年定价,bj示北京,sh表示上海。提供Q单位服务的成本为:C=1 000+30Q,其中,Q=Qbj+Qsh (1)北京市场和上海市场的利润最大化价格和数量各是多少? (2)由于部署了一颗新卫星,使得上海人可以接收到公司在北京发送的节目,而北京人也可接收到公司在上海的播出节目。这样北京或上海的任何人只要在任意城市付费就可接收到公司的节目。因此公司只能定单一的价格。它会定什么价格?它在北京和上海的销售数量分别为多少? (3)公司更加偏爱上面的哪种情况,(1)还是(2)?从消费者剩余的角度,北京人偏爱哪种情况而上海人偏爱哪种情况?为什么?
参考答案
参考解析
解析:(1)由两个市场的需求函数可得相应的反需求函数为:
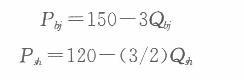
该公司利润函数为:
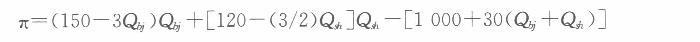
利润最大化的一阶条件为:
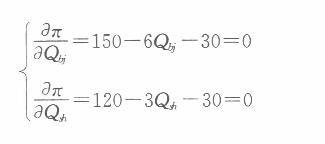
解得:Qbj =20,Qsh=30。 将数量代入各自的需求函数可得在北京市场,利润最大化的价格为90;在上海市场,利润最大化的价格为75。 (2)当两地统一定价时,此时市场需求函数为: Q=Qbj+Qsh=50-(1/3)P+80-(2/3)P=130-P 得反需求函数为: P=130-Q 该公司利润函数为: 兀=(130 - Q) Q-(1000+30Q)一Q2+100Q一1 000 利润最大化的一阶条件为:
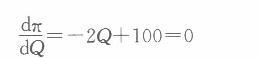
解得产量为50,价格为80。将价格为80代入两个市场的需求函数可得北京市场需求量为(70/3),上海市场需求量为(80/3)。 (3)当分别定价时,公司利润为: PQ-C=20×90+30×75-[1 000+30×(30+20)]=1 550 当统一定价时,公司利润为: PQ-C=80×50-(1 000-1-30×50) =1 500 可以看出,分别定价时,公司利润大。 从消费者剩余角度考虑。分别定价时,北京的消费者剩余为(150-90)×20/2—600,上海的消费者剩余为(120- 75)×30/2—675。单一定价时,北京消费者剩余为(150 - 80)*(70/3)/2≈816.6,上海消费者剩余为(120-80)*(80/3)/2≈533.3。因此,上海人偏爱分别定价,北京人偏爱单一定价。
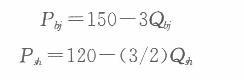
该公司利润函数为:
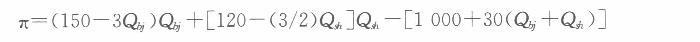
利润最大化的一阶条件为:
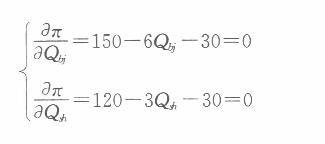
解得:Qbj =20,Qsh=30。 将数量代入各自的需求函数可得在北京市场,利润最大化的价格为90;在上海市场,利润最大化的价格为75。 (2)当两地统一定价时,此时市场需求函数为: Q=Qbj+Qsh=50-(1/3)P+80-(2/3)P=130-P 得反需求函数为: P=130-Q 该公司利润函数为: 兀=(130 - Q) Q-(1000+30Q)一Q2+100Q一1 000 利润最大化的一阶条件为:
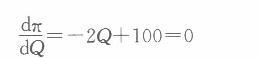
解得产量为50,价格为80。将价格为80代入两个市场的需求函数可得北京市场需求量为(70/3),上海市场需求量为(80/3)。 (3)当分别定价时,公司利润为: PQ-C=20×90+30×75-[1 000+30×(30+20)]=1 550 当统一定价时,公司利润为: PQ-C=80×50-(1 000-1-30×50) =1 500 可以看出,分别定价时,公司利润大。 从消费者剩余角度考虑。分别定价时,北京的消费者剩余为(150-90)×20/2—600,上海的消费者剩余为(120- 75)×30/2—675。单一定价时,北京消费者剩余为(150 - 80)*(70/3)/2≈816.6,上海消费者剩余为(120-80)*(80/3)/2≈533.3。因此,上海人偏爱分别定价,北京人偏爱单一定价。
更多 “华强卫星公司向北京和上海的订户发送电视节目,两地订户群体的需求曲线分别为: Qbj =50-(1/3)Pbj,Qsh =80- (2/3)Psh式中,Q以年千户计,P是年定价,bj示北京,sh表示上海。提供Q单位服务的成本为:C=1 000+30Q,其中,Q=Qbj+Qsh (1)北京市场和上海市场的利润最大化价格和数量各是多少? (2)由于部署了一颗新卫星,使得上海人可以接收到公司在北京发送的节目,而北京人也可接收到公司在上海的播出节目。这样北京或上海的任何人只要在任意城市付费就可接收到公司的节目。因此公司只能定单一的价格。它会定什么价格?它在北京和上海的销售数量分别为多少? (3)公司更加偏爱上面的哪种情况,(1)还是(2)?从消费者剩余的角度,北京人偏爱哪种情况而上海人偏爱哪种情况?为什么?” 相关考题
考题
某成本不变的完全竞争行业的代表性厂商的长期总成本函数为LTC=Q3-60Q2+1500Q,产品价格P=975美元,市场需求函数为P=9600-2Q,试求:(1)利润极大时的产量、平均成本和利润。(2)该行业长期均衡时的价格和厂商的产量。(3)用图形表示上述(1)和(2)。(4)若市场需求曲线是P=9600-2Q,试问长期均衡中留存于该行业的厂商人数是多少?
考题
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求:(1)当市场商品价格是P=100,厂商实现MR=LMC时的产量,平均成本和利润;(2)该行业长期均衡时的价格和单个厂商的产量;(3)市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。
考题
已知完全竞争市场上单个厂商的长期成本函数为LTC=Q3-20Q2+200Q,市场的产品价格为P=600。 求:(1)该厂商实现利润最大化时的产量、平均成本和利润各是多少? (2)该行业是否处于长期均衡,为什么?(3)该行业处于长期均衡时每个厂商的产量、平均成本和利润各是多少? (4)判断(1)中的厂商是处于规模经济阶段,还是处于规模不经济阶段?
考题
某企业生产产品的边际成本是个常数,为每件20元(即MC=AC=20元/件)。该企业将市场细分为三个价格弹性明显差异并且企业能有效控制价格的市场。这三个市场的需求曲线分别为:市场1,P1=1520-3Q1;市场2,P2=1220-2Q2;市场3,P3=1020–Q3求:能使利润最大化的三个市场的销售量和价格。参考答案:解:据三个市场的需求曲线,可分别求得三个市场的总收入TR曲线和边际收入MR曲线:TR1=P1Q1=1520Q1-3Q12; MR1=1520-6Q1TR2=P2Q2=1220Q2-2Q22;MR2=1220-4Q2TR3=P3Q3=1020Q3-Q32;MR3=1020-2Q3根据差别定价最优化(能使利润最大化)的条件:MR1=MR2=MR3=MC有:MR1=MC,即1520-6Q1=20,得市场1的销售量Q1=250件MR2=MC,即1220-4Q2=20,得市场2的销售量Q2=300件MR3=MC,即1020-2Q3=20,得市场3的销售量Q2=500件代入各需求方程得:市场1的价格P1=1520-3Q1=1520-3参考答案:×250=770(元/件)市场2的价格P2=1220-2Q2=1220-2
考题
北京公司与上海公司在贸易洽谈会上达成订立合同的初步意向。洽谈会结束后,北京公司于8月7日以信件方式(当日邮戳)向上海公司正式发出要约,欲以一定价格出售一批机器给上海公司,并言明,上海公司可在10日内答复。信件内未载明日期。上海公司于8月9日收到该信件。因此时上海公司正与宁波公司磋商合同订立事宜,及至8月18日,因与宁波公司的磋商失败,才急忙向北京公司用传真发出承诺通知。北京公司收到传真后,未做任何表示。后因双方对合同是否成立发生纠纷。对此,下列表述中正确的是:
A.上海公司的通知为有效承诺,因其未过承诺期限
B.上海公司的通知为有效承诺,因北京公司未做任何表示
C.上海公司的通知为新要约,但北京公司不做任何表示,视为承诺,故合同成立
D.上海公司的通知为新要约,北京公司不做任何表示,故合同未成立
考题
生产差别产品的两个厂商通过选择价格竞争,他们的需求曲线分别为Q1=20-p1+ p2和Q2= 20—P2+P1,其中p1和P2是两个厂商的定价,Q1和Q2则是相应的需求一假设成本为零。 (1)若两个厂商同时决定价格,那么他们会定什么价格,销量和利润各为多少? (2)设厂商1先定价格,然后厂商2定价。厂商1观测到了厂商2的反应曲线,这时各厂商将定价多少,销量和利润为多少?
考题
一个行业包括一个主导厂商(用z表示)和12个次要厂商(用j表示).主导厂商的总成本函数为Ci=0.0333q3-2q2 +50q,,市场需求曲线为Q=250 -p:主导厂商准确地估计出每个小厂商的成本函数为C.= 2q2+ 1Oq,。主导厂商领导市场价格,并管理自己的产出量,使整个市场供给既不短缺,也无剩余。主导厂商能够正确地预期次要厂商将接受它定的价格。主导厂商的定价是为了使自己的利润最大。 (1)主导厂商的定价为多高?它的产量和利润分别为多少? (2)每个小企业的产量和利润分别为多少?
考题
假设某大宗商品的国际需求函数Q=a-P。两个寡头公司1和2向该市场提供同质产品,拥有不变的单位边际成本,分别为c1和c2,且有a>c2 >c1。 若两个公司展开古诺(Cournot)竞争,则各自的纳什均衡产量q1和q2是多少?
考题
假定某寡头厂商面临一条弯折的需求曲线,产量在0~30单位范围内时需求函数为P=60-0.3Q,产量超过30单位时需求函数为P=66 -0.50;该厂商的短期总成本函数为STC=0.005 Q3-0. 2Q2 +36Q +200。 (1)求该寡头厂商利润最大化的均衡产量和均衡价格。 (2)假定该厂商成本增加,导致短期总成本函数变为STC =0.005Q3 -0.2Q2 +50Q +200,求该寡头厂商利润最大化的均衡产量和均衡价格。 (3)对以上(1)和(2)的结果作出解释。
考题
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数为LTC= Q3 - 12Q2+40Q。试求: (1)当市场产品价格为P=100时,厂商实现MR= LMC时的产量、平均成本和利润。 (2)该行业长期均衡时的价格和单个厂商的产量。 (3)当市场的需求函数为Q=660 -15P时,行业长期均衡时的厂商数量。
考题
考虑一个双寡头古诺模型,p和Q分别表示市场价格和产品销售总量;q1和q2分别表示厂商1和厂商2的产量;MC表示厂商生产的边际成本,假设两个厂商生产的产品完全同质。 如果两个厂商的生产均面临不变的边际成本1/2,且反需求曲线为p=1-Q,则均衡时两个企业的产量分别是多少?
考题
已知某垄断厂商的短期总成本函数为STC =0. 6Q2+3Q +2,反需求函数为P=8 -0. 4Q: (1)求该厂商实现利润最大化时的产量、价格、收益和利润。 (2)求该厂商实现收益最大化时的产量、价格、收益和利润。 (3)比较(1)和(2)的结果。
考题
一个完全竞争行业中的一个典型厂商,其长期总成本函数为LTC =q3- 60q2+1500q,其中成本的单位为元,q为月产量. (1)推导出其长期平均成本和长期边际成本函数。 (2)若产品市场价格为975元,为实现利润最大化,厂商的产量将是多少? (3)厂商在(2)中的均衡是否与行业均衡并存? (4)若市场的需求曲线为P=9600 -Q,在长期均衡中,该行业将有多少厂商?
考题
一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3(Q1+Q2),东部市场对该产品的需求函数为P1=15-Q1,西部市场对该产品的需求函数为P2=25一2Q2。 如果政府规定,禁止在不同市场上制定不同的价格,求此时该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。
考题
市场反需求函数为P=a-bQ,有N(N≥3)个同质企业,典型企业i的成本函数为TC(qi)=Qqi,其中Q为市场的总产量,且Q=(q1+q2…+qx)。 假设价格为P,求N个企业进行古诺竞争时每个企业的产量和利润,以及市场总产量和总利润。
考题
一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3(Q1+Q2),东部市场对该产品的需求函数为P1=15-Q1,西部市场对该产品的需求函数为P2=25一2Q2。 如果该厂商可以将东西部市场区分开,在不同的市场制定不同的价格出售,求该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。
考题
某通信公司提供两项通信业务,分别为业务A和业务B。经过成本分析和归集,两项业务的成本总额分别为a1,a2,两项业务的业务量分别为q1,q2。
如果业务A的目标利润为r,采用成本加成定价,则单位产品价格P为()A.P=a1+r
B.P=(a1+r)/q1
C.P=a1(1+r)
D.p=a1(1+r)/q1
考题
一个歧视性垄断厂商在两个市场上销售,假设不存在套利机会,市场1的需求曲线为P1=100-Q1/2,而P2=100-Q2,垄断厂商的总产量用Q=Q1+Q2表示,垄断厂商的成本函数依赖于总产出,TC(Q)=Q2。在利润最大化时,下列说法正确的是( )。
Ⅰ.垄断厂商在市场1的产量Q1为30
Ⅱ.垄断厂商在市场2的产量Q2为12.5
Ⅲ.歧视性垄断的利润水平是1875
Ⅳ.垄断厂商的总产量为37.5
A.Ⅱ、Ⅲ、Ⅳ
B.Ⅰ、Ⅱ
C.Ⅰ、Ⅱ、Ⅲ、Ⅳ
D.Ⅰ、Ⅲ、Ⅳ
考题
已知某完全垄断企业的需求函数为P=17-4Q,成本函数为TC=5Q+2Q2。 (1)计算企业利润最大化的价格和产出、利润。 (2)如果政府实行价格管制,按边际成本定价与按平均成本定价,价格分别是多少?厂商是否亏损?
考题
出生于深圳的公民小张的户籍在上海,但由于工作的原因,他经常居住北京,已达2年多。依照法律规定()。A、深圳、上海和北京都是小张的住所B、上海和北京是小张的住所C、北京为小张的住所D、上海视为小张的住所,北京是小张的住所
考题
某客户在搜索推广的账户层级设定了推广地域为北京、河北,为计划1设定推广地域为北京、上海,计划2未设置推广地域,则计划2的实际投放地区是:()A、北京、上海、河北B、北京、上海C、北京、河北D、北京
考题
问答题已知完全竞争市场上单个厂商的长期成本函数为LTC=Q3-20Q2+200Q,市场的产品价格为P=600。 求:(1)该厂商实现利润最大化时的产量、平均成本和利润各是多少? (2)该行业是否处于长期均衡,为什么?(3)该行业处于长期均衡时每个厂商的产量、平均成本和利润各是多少? (4)判断(1)中的厂商是处于规模经济阶段,还是处于规模不经济阶段?
考题
问答题某垄断者的产品在两个分割市场出售,产品的成本函数和两个市场的需求函数分别为TC=Q2+10Q,Q1=32-0.4P1,Q2=18-0.1P2,其中Q=Q1+Q2。 (1)假设两个市场能实行差别价格,求解利润最大时的两个市场的售价、销售量和利润。 (2)假设两个市场只能索取相同价格,求解利润最大时的售价、销售量和利润。
热门标签
最新试卷