网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
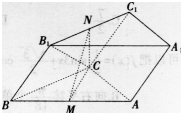
如图,三棱柱ABC-A1B1C1,M,N分别为AB,B1C1的中点,
(1)求证MN∥平面AA1C1C;
(2)若C1C=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB⊥平面CMN。
(1)求证MN∥平面AA1C1C;
(2)若C1C=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB⊥平面CMN。

参考答案
参考解析
解析:

更多 “如图,三棱柱ABC-A1B1C1,M,N分别为AB,B1C1的中点, (1)求证MN∥平面AA1C1C; (2)若C1C=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB⊥平面CMN。 ” 相关考题
考题
一条路上依次有A、B、C三个站点,加油站M恰好位于AC的中点,加油站N恰好位于BC的中点,若想知道M和N两个加油站之间的距离,只需发知道哪两点之间的距离?A.BCB.CNC.AMD.AB
考题
如图,正四面体P-ABC的棱长为a,D、E、F分别为PA、PB、PC的中点,G、H、M 分别为DE,EF,FD的中点,则三角形GHM的面积与正四面体P-ABC的表面积之比为( )。
A. 1 : 8
B. 1 : 16
C. 1 : 32
D. 1 : 64
考题
三个重物m1、m2、m3用一绕过两个定滑轮M和N的绳子相连,如图所示。当重物m1下降时,重物m2在四棱柱ABCD的上面向右移动,而重物m3则沿侧面AB上升。若三个重物的质量均为M;四棱柱的质量为9M,它置于水平光滑面上,开始物系静止。当重物m1下降h时,四棱柱的位移为( )。
考题
—条路上依次有A、B、C三个站点,加油站M恰好位于A、C的中点,加油站N恰好位于B、C的中点,若想知道M和N两个加油站之间的距离,只需要知道哪两点之间的距离?( )
A. CN
B. BC
C. AM
D. AB
考题
一条路上依次有A、B、C三个站点,加油站M恰好位于AC的中点,加油站N恰好位于BC的中点。若想知道M和N两个加油站之间的距离,只需要知道哪两点之间的距离?()
A. CN B. BC C. AM D. AB
考题
假定AB跨(即左端边跨)按荷载效应标准组合并考虑长期作用影响的跨中最大弯矩截面的刚度和B支座处的刚度,依次分别为B1=8.41013Nmm2,B2=6.51013Nmm2,作用在梁上的永久荷载标准值qGk=15kN/m,可变荷载标准值qQk=30kN/m。试问,AB跨中点处的挠度值f(mm),与下列何项数值最为接近?( )
(提示:在不同荷载分布作用下,AB跨中点挠度计算式如图)
A、20、5
B、22、6
C、30、4
D、34、2
考题
某钢筋混凝土五跨连续梁,其计算简图及B支座配筋如图2-1所示:混凝土强度等级为C30,ft=1.43N/mm2,ftk=2.01N/mm2,Ec=3.0×10^4N/mm2;纵筋采用HRB400级热轧钢筋,Es=2.0×10^5N/mm2。
假定AB跨(即左端边跨)按荷载效应标准组合并考虑长期作用影响的跨中最大弯矩截面的刚度和B支座处的刚度,依次分别为B1=8.4×10^13N·mm2,B2=6.5×10^13N·mm2,作用在梁上的永久荷载标准值qGk=15kN/m,可变荷载标准值qQk=30kN/m。AB跨中点处的挠度值f(mm)最接近于下列( )项数值。 提示:在不同荷载分布作用下,AB跨中点挠度计算式如图所示。
A. 20.5
B. 22.6
C. 30.4
D. 34.2
考题
如图所示,真空中有A、B两个等量异种点电荷,0、M、N是AB连线的垂线上的三个点,且A O>OB。一个带负电的检验电荷仅在电场力的作用下,从M点运动到N点,其轨迹如图中实线所示。若M、N两点的电势分别为M和N,检验电荷通过M、Ⅳ两点的动能分别为Ekm和Ekn,则( )。
考题
如图,α⊥β,α∩β=l,A∈α,B∈β,A,B到l的距离分别是a和b, AB与a,β所成的角分别是θ和φ,AB在α,β内的射影分别是m和n,若a>b,则( )。
A、θ>φ,m>n
B、θ>φ,mC、θD、θn
考题
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。
考题
(10分)如图,几何体A1B1C1-ABC中,AB=AC,AB⊥AC,棱AA1,BB1,CC1都垂直于面ABC,BC=AA1=2BB1=2CC1=4,D为B1C1的中点,E为A1D的中点。
求证:(1)AE⊥BC;(3分)
(2)求异面直线AE与DC所成角的余弦值。(7分)
考题
单选题设A是m×n矩阵,B是n×m矩阵,则( )。A
当m>n时,必有|AB|≠0B
当m>n时,必有|AB|=0C
当n>m时,必有|AB|≠0D
当n>m时,必有|AB|=0
热门标签
最新试卷