网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
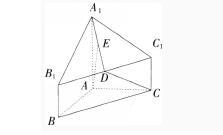
(10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。
求证：(1)AE⊥BC；(3分)
(2)求异面直线AE与DC所成角的余弦值。(7分)

参考答案

参考解析
解析：
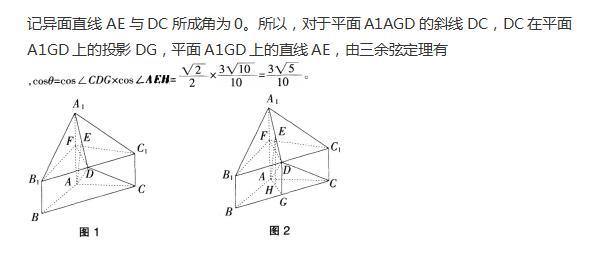
更多 “(10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。 求证：(1)AE⊥BC；(3分) (2)求异面直线AE与DC所成角的余弦值。(7分) ” 相关考题
考题 △ABC中，AB=3，BC=4，则AC边的长满足（ ）。A．AC=5B．AC1C．AC7D．1AC7
查看答案
考题 有如下嵌套的if语句： if(ab) if(ac)k=a； else k=C： else if(bc)k=b； else k=C； 以下选项中与上述if语句等价的语句是（ ）。A.k=(ab)?a：b；k=(bc)?b：C；B.k=(ab)?((bc)?a：b)：((bc)?b：c)；C.k=(ab)?((ac)?a：c)：((bc)?b：c)；D.k=(ab)?a：b；k=(ac)?a：c；
查看答案
考题 在 △ABC中，∠C=90°，AB=10。（1）∠A=30°，求BC，AC（精确到0.01）；（2）∠A=45°，求BC，AC（精确到0.01）。
查看答案
考题 △ABC中，AB=13cm，BC=10cm，BC边上的中线AD=12cm.求AC
查看答案
考题 在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。A．2.5B．5C．10D．15
查看答案
考题 试证明如下逻辑函数等式。(1) AB－＋AB－C=AB－;(2) AB(C＋C－)＋AC=AB＋AC;(3) A(BC＋BC)＋AC=A(BC)＋AC
查看答案
考题 试用卡诺图化简如下逻辑函数式。(1) Y1=ABC＋ABC－＋B－(2) Y2=A＋AB－C＋AB(3) Y3=AC－＋AB－＋AB(4) Y4=AB－C－＋AC－＋C
查看答案
考题 设A、B、C为随机事件，则( )。A.P(A-B-C)=P(A)-P(AB)-P(AC)-P(BC)+P(ABC) B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC) C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC) D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)
查看答案
考题 如图2-7所示，三棱镜ABC，∠A=30°.光线垂直AB面射入棱镜，由AC面射出.已知出射光与入射光的夹角为30°.在Ac面上光线的入射角是（），棱镜的折射率是（）.
查看答案
考题 如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。 A.12 B.14 C.15 D.16
查看答案
考题 如图，Rt△ABC中，∠ABC=90o,AB=28 cm，以AB为直径的半圆与AC相交，图中的阴影部分①的面积比⑦的面积少28.28 cm2，求BC的长(π取3．14)。
查看答案
考题 如图，三棱柱ABC-A1B1C1，M，N分别为AB，B1C1的中点， (1)求证MN∥平面AA1C1C； (2)若C1C=CB1，CA=CB，平面CC1B1B⊥平面ABC，求证：AB⊥平面CMN。
查看答案
考题 在△ABC中，已知AB＝5，AC＝3，∠A＝120°，则BC长为
查看答案
考题 在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．
查看答案
考题 在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．
查看答案
考题 在 ABC中，∠ABC=600，AB=4，BC=6，则AC=（）
查看答案
考题 在三角形ABC，AB=4，AC=6，BC=8，D为BC的中点，则AD=
查看答案
考题 如图所示，有一束平行于等边三棱镜截面ABC的单色光从空气射向E点，并偏折到F点。已知入射方向与边AB的夹角为θ=30。，E、F分别为边AB、BC的中点，则（　　）。
查看答案
考题 已知△ABC的三边长AC＝3，BC＝4，AB＝5，P为AB边上任意一点，则CP→ (BA→－BC→)的最大值为(　　)A、8 B、9 C、12 D、15
查看答案
考题 如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）A、6cm　 B、8cm C、10cm　　 D、12cm
查看答案
考题 如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。
查看答案
考题 如图，已知四棱锥P-ABCD底面ABCD为矩形，侧棱PA⊥ABCD，AB=AP=21/2AD=2，E，F分别为PC，AB的中点。 (I)证明：EF∥面PAD。 (II)求三棱锥B-PFC的体积。
查看答案
考题 如图，正方体ABCD-A1B1C1D1中，E，F，G分别为AA1，A1D1，BC的中点，则异面直线EF与D1G所成角的大小为__________。
查看答案
考题 逻辑函数Y=ABC+AC+BC的最简式为（）A、Y=CB、Y=BC+AB+BCC、Y=ABC+AC+BCD、Y=1
查看答案
考题 有一镗削工件，三孔ABC的坐标尺寸如图，为检验上的需要，计算三孔ABC的中心距尺寸，正确的是（）。A、AB=26.93，BC=23.35，AC=27.2B、AB=26.93，BC=20.23，AC=26.5C、AB=25.03，BC=23.35，AC=27.2D、AB=25.03，BC=20.23，AC=27.2
查看答案
考题 Y=AB+BC+A=（）。A、A+BCB、AC、BCD、ABC
查看答案
考题 单选题如图所示，力P作用在BC杆的中点，且垂直于BC杆，若P=kN，杆重不计。则杆AB的内力大小S为（　）A 1kNB 0．5kNC 1．41kND 2kN
查看答案
热门标签
最新试卷