网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设y=f(x)是(a,b)内的可导函数,x,x+△x是(a,b)内的任意两点,则:
A. △y=f’(x)△x
B.在x,x+△x之间恰好有一点ξ,使△y=f’(ξ)△x
C.在x,x+△x之间至少存在一点ξ,使△y=f’(ξ)△x
D.在x,x+△x之间的任意一点ξ,使△y=f’(ξ)△x
B.在x,x+△x之间恰好有一点ξ,使△y=f’(ξ)△x
C.在x,x+△x之间至少存在一点ξ,使△y=f’(ξ)△x
D.在x,x+△x之间的任意一点ξ,使△y=f’(ξ)△x
参考答案
参考解析
解析: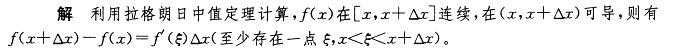
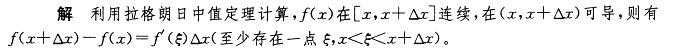
更多 “设y=f(x)是(a,b)内的可导函数,x,x+△x是(a,b)内的任意两点,则: A. △y=f’(x)△x B.在x,x+△x之间恰好有一点ξ,使△y=f’(ξ)△x C.在x,x+△x之间至少存在一点ξ,使△y=f’(ξ)△x D.在x,x+△x之间的任意一点ξ,使△y=f’(ξ)△x ” 相关考题
考题
以下结论正确的是()。
A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
考题
以下程序段的执行结果为【】。includedefine PLUS(x, y) x+ yvoid main() { int x=1, y
以下程序段的执行结果为【 】。include<iostream.h>define PLUS(x, y) x+ yvoid main(){int x=1, y=2,z=3,sum;sum=PLUS(x+ y, z)*PLUS(y, z);cout<<"SUM="<<sum;cout<<end1;}
考题
设x和y均为int型变量,则执行下面的循环后,y值为()。include void main(){int x, y;f
设x和y均为int型变量,则执行下面的循环后,y值为( )。#include <iostream.h>void main(){int x, y;for(y= 1,x= 1 ;y<=50;y++){ if(x>=10) }break;if (x%2==1){ x+=5; continue;} x-=3;} cout<<y;A.2B.4C.6D.8
考题
设以下变量均为int类型,则值不等于7的表达式是( )。A.(x=y=6,x+ y,x+1)B.(x=y=6,x +y,y+1)C.(x=6,x+1,y=6,x +y)D.(y=6,y+1,x=y,x+1)
考题
设f(x),f'(x)为已知的连续函数,则微分方程y'十f'(x)y=f(x)f'(x)的通解是:
A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +c
C. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)
考题
设y=f(x)是(a, b)内的可导函数,X,X+ΔX是(a, b)内的任意两点,则:
(A) Δy= f‘ (x)Ax
(B)在x,x+Ax之间恰好有一点ξ,使Δy=f'(ξ)Ax
(C)在x, x+Ax之间至少有一点ξ,使Δy=f'(ξ)Ax
(D)对于x,x+ax之间任意一点ξ,使Δy=f'(ξ)Ax
考题
下列结论正确的是( ).A.x=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件
B.z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件
C.z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件
D.z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
下列( )项是在D={(x,y)|x2+y2≤1,x≥0,y≥0)上的连续函数f(x,y),且f(x,y)=3(x+y)+16xy。
A.f(x,y)=3(x+y)+32xy
B.f(x,y)=3(x+y)-32xy
C.f(x,y)=3(x+y)-16xy
D.f(x,y)=3(x+y)+16xy
考题
设y=f(x)是(a,b)内的可导函数,x,x+△x是(a,b)内的任意两点,则:
A. △y=f’(x)△x
B.在x,x+△x之间恰好有一点ξ,使△y=f’(ξ)△x
C.在x,x+△x之间至少存在一点ξ,使△y=f’(ξ)△x
D.在x,x+△x之间的任意一点ξ,使△y=f’(ξ)△x
考题
设y=f(x)是(a,b)内的可导函数,x和x+Δx是(a,b)内的任意两点,则:
A. Δy=f' (x)Δx
B.在x,x+Δx之间恰好有一点ξ,使Δy=f' (ξ)Δx
C.在x,x+Δx之间至少有一点ξ,使Δy=f' (ξ)Δx
D.在x,x+Δx之间任意一点ξ,使Δy=f' (ξ)Δx
考题
A.f(-x,y)=f(x,y),f(x,-y)=-f(x,y)
B.f(-x,y)=f(x,y),f(x,-y)=f(x,y)
C.f(-x,y)=-f(x,y),f(x,-y)=-f(x,y)
D.f(-x,y)=-f(x,y),f(x,-y)=f(x,y)
考题
下列结论不正确的是()。A、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处连续B、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处可导C、z=f(x,y)在点(x0,y0)处可导,则f(x,y)在点(x0,y0)处可微D、z=f(x,y)在点(x0,y0)处偏导数连续,则f(x,y)在点(x0,y0)处连续
考题
下列结论正确的是().A、x=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B、z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C、z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D、z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
下列结论不正确的是()。A、y=f(x)在点x0处可微,则f(x)在点x0处连续B、y=f(x)在点x0处可微,则f(x)在点x0处可导C、y=f(x)在点x0处连续,则f(x)在点x0处可微D、y=f(x)在点x0处可导,则f(x)在点x0处连续
考题
下列结论正确的是().A、z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B、z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C、z=(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D、z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
单选题以下关于二元函数的连续性的说法正确是( )。A
若f(x,y)沿任意直线y=kx在点x=0处连续,则f(x,y)在(0,0)点连续B
若f(x,y)在点(x0,y0)点连续,则f(x0,y)在y0点连续,f(x,y0)在x0点连续C
若f(x,y)在点(x0,y0)点处偏导数fx′(x0,y0)及fy′(x0,y0)存在,则f(x,y)在(x0,y0)处连续D
以上说法都不对
考题
单选题下列结论正确的是().A
z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B
z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C
z=(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D
z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
单选题若函数f(x)在区间(a,b)内可导,x1和x2是区间(a,b)内任意两点(x1<x2),则至少存在一点ξ,使( )A
f(b)-f(a)=f′(ξ)(b-a)(a<ξ<b)B
f(b)-f(x1)=f′(ξ)(b-x1)(x1<ξ<b)C
f(x2)-f(x1)=f′(ξ)(x2-x1)(x1<ξ<x2)D
f(x2)-f(a)=f′(ξ)(x2-a)(a<ξ<x2)
考题
单选题(2009)设y=f(x)是(a,b)内的可导函数,x+△x是(a,b)内的任意两点,则:()A
△y=f′(x)△xB
在x,x+△x之间恰好有一点ξ,使△y=f′(ξ)△xC
在x,x+△x之间至少有一点ξ,使△y=f′(ξ)△xD
在x,x+△x之间任意一点ξ,使△y=f′(ξ)△x
考题
单选题若z=f(x,y)和y=φ(x)均可微,则dz/dx等于( )。[2013年真题]A
∂f/∂x+∂f/∂yB
∂f/∂x+(∂f/∂y)(dφ/dx)C
(∂f/∂y)(dφ/dx)D
∂f/∂x-(∂f/∂y)(dφ/dx)
考题
单选题下列结论正确的是().A
x=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B
z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C
z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D
z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
单选题设f(x)在(-∞,+∞)可导,x0≠0,(x0,f(x0))是y=f(x)的拐点,则( )。A
x0必是f′(x)的驻点B
(-x0,-f(x0))必是y=-f(-x)的拐点C
(-x0,-f(x0))必是y=-f(x)的拐点D
对∀x>x0与x<x0,y=f(x)的凸凹性相反
考题
单选题设函数z=z(x,y)由方程F(x-az,y-bz)=0所给出,其中F(u,v)任意可微,则a∂z/∂x+(b∂z/∂y)=( )。A
0B
1C
2D
4
热门标签
最新试卷