网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的两倍减去2,其中x>1,y>0。则当y x=1=1时的曲线方程为:


参考答案
参考解析
解析:提示:把方程变形,得到可分离变量的方程,求通解、特解。解法如下:
y3=2(y-xy') ,y3=2y-2xy', 2xy'=2y-y3

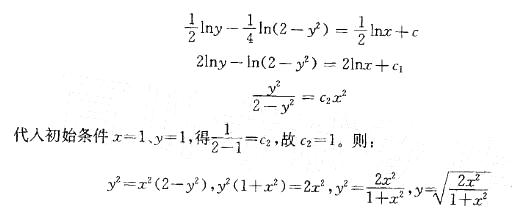
y3=2(y-xy') ,y3=2y-2xy', 2xy'=2y-y3

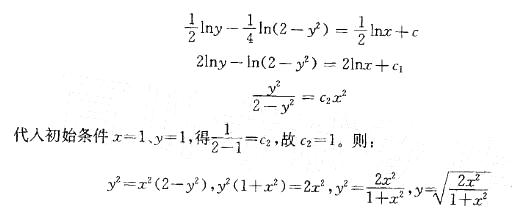
更多 “曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的两倍减去2,其中x>1,y>0。则当y x=1=1时的曲线方程为: ” 相关考题
考题
设曲线y=f(x)上任一点(x,y)处的切线斜率为(y/x)+x2,且该曲线经过点(1,1/2)。(1)求函数y=f(x);(2)求由曲线y= f(x),y=O,x=1所围图形绕x轴旋转一周所得旋转体的体积V。
考题
如果曲线y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( )。A. y=x3-2B. y=2x3-5C. y=x2-2D. y=2x2-5
考题
曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的两倍减去2,其中x> 1,y>0。曲线y =f(x)所满足的微分方程应是:
A. y3=2(y-xy') B. 2xy'=2y
C. 2xy'=-y3 D. 2xy=2y+y3
考题
如果曲线Y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( ).A.Y=3-2
B.Y=2x3-5
C.Y=x2-2
D.Y=2x2-5
考题
曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的二倍减去2,其中x1,y0。曲线y=f(x)所满足的微分方程应是:()A、y3=2(y-xy′)B、2xy′=2yC、2xy′=-y3D、2xy=2y+y3
考题
单选题曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的二倍减去2,其中x1,y0。曲线y=f(x)所满足的微分方程应是:()A
y3=2(y-xy′)B
2xy′=2yC
2xy′=-y3D
2xy=2y+y3
考题
单选题若曲线C上点的坐标都是方程f(x,y)=0的解,则下列判断中正确的是( ).A
曲线C的方程是f(x,y)=0B
以方程f(x,y)=0的解为坐标的点都在曲线C上C
方程f(x,y)=0的曲线是CD
方程f(x,y)=0表示的曲线不一定是C
考题
单选题设函数y=f(x)由方程e2x+y-cos(xy)=e-1所确定,则曲线y=f(x)在点(0,1)处的法线方程为( )。A
y+1=x/2B
y-1=x/2C
y+1=xD
y-1=x
考题
单选题函数y=f(x)是由方程xy+2lnx=y4所确定,则曲线y=f(x)在点(1,1)处的切线方程为( )。A
x-y=0B
x+y=0C
-x-y=0D
-x+y=0
热门标签
最新试卷