网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
f(x)=|x-2|在点x=2的导数为()
A.1
B.0
C.-1
D.不存在
B.0
C.-1
D.不存在
参考答案
参考解析
解析: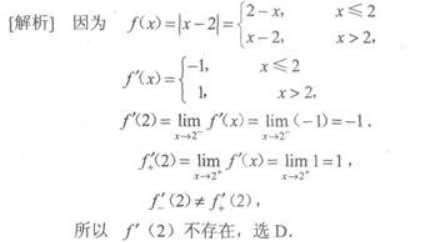
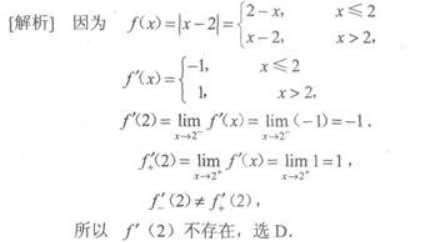
更多 “f(x)=|x-2|在点x=2的导数为()A.1 B.0 C.-1 D.不存在” 相关考题
考题
以下结论正确的是()。
A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
考题
有以下程序includeint f(intx){inty; if(x==0||x==1)return(3); y=x*x-f(x-2); return
有以下程序 #include <stdio.h> int f(int x) { int y; if(x==0||x==1) return(3); y=x*x-f(x-2); return y; } main() { int z; z=f(3); printf("%d\n",z); } 程序的运行结果是A.0B.9C.6D.8
考题
下列结论正确的是( ).A.x=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件
B.z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件
C.z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件
D.z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
函数厂(x)具有连续的二阶导数,且f″(0)≠0,则x=0( )。A.不是函数f(x)的驻点
B.一定是函数f(x)的极值点
C.一定不是函数f(x)的极值点
D.是否为函数f(x)的极值点,还不能确定
考题
下列命题正确的是()A.函数f(x)的导数不存在的点,一定不是f(x)的极值点
B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0
D.若函数f(x)在点x0处连续,则f'(x0)一定存在
考题
设函数f(x)在定义域I上的导数大于零,若对任意的x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)的表达式.
考题
若f″(x)存在,则函数y=ln[f(x)]的二阶导数为:()A、(f″(x)f(x)-[f′(x)]2)/[f(x)]2B、f″(x)/f′(x)C、(f″(x)f(x)+[f′(x)]2)/[f(x)]2D、ln″[f(x)]·f″(x)
考题
下列结论正确的是().A、x=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B、z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C、z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D、z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
下列结论正确的是().A、z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B、z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C、z=(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D、z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
问答题设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f″(x)|≤b(其中a、b都是非负常数),c是(0,1)内任一点。 (1)写出f(x)在点x=c处带拉格朗日余项的一阶泰勒公式; (2)证明:|f′(c)|<2a+b/2。
考题
单选题若f″(x)存在,则函数y=ln[f(x)]的二阶导数为:()A
(f″(x)f(x)-[f′(x)]2)/[f(x)]2B
f″(x)/f′(x)C
(f″(x)f(x)+[f′(x)]2)/[f(x)]2D
ln″[f(x)]·f″(x)
考题
单选题考虑二元函数f(x,y)的下面4条性质:①f(x,y)在点(x0,y0)处连续;②f(x,y)在点(x0,y0)处的两个偏导数连续;③f(x,y)在点(x0,y0)处可微;④f(x,y)在点(x0,y0)处的两个偏导数存在。若用“P⇒Q”表示可由性质P推出Q,则有( )。A
②⇒③⇒①B
③⇒②⇒①C
③⇒④⇒①D
③⇒①⇒④
考题
单选题下列结论正确的是().A
x=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B
z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C
z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D
z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
考题
单选题设f(x)=x(x-1)(x-2),则方程f'(x)=0的实根个数是:A
3B
2C
1D
0
热门标签
最新试卷