网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
以.
为通解的二阶线性常系数齐次微分方程为_____
为通解的二阶线性常系数齐次微分方程为_____参考答案
参考解析
解析：所给问题为求解微分方程的反问题．常见的求解方法有两种：解法1先由通解写出二阶线性常系数齐次微分方程的特解，再由此写出方程的特征根r1，
r2，第三步写出特征方程(r-r1)(r-r2)=0，再依此写出相应的微分方程；
解法2由所给方程的通解，利用微分法消去任意常数，得出微分方程．这里只利用解法1求解．由于二阶线性常系数齐次微分方程的通解为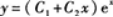
，由其解的结构定理可知方程有两个特解：
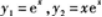，从而知道特征方程的二重根r=1．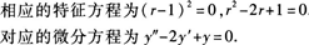
r2，第三步写出特征方程(r-r1)(r-r2)=0，再依此写出相应的微分方程；
解法2由所给方程的通解，利用微分法消去任意常数，得出微分方程．这里只利用解法1求解．由于二阶线性常系数齐次微分方程的通解为
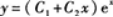，由其解的结构定理可知方程有两个特解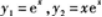：，从而知道特征方程的二重根r=1．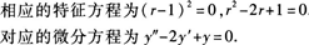
更多 “以.为通解的二阶线性常系数齐次微分方程为_____” 相关考题
考题
以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是：
A. y"-2y'-3y=0
B. y"+2y'-3y=0
C. y"-3y'+2y=0
D. y"+2y'+y=0
考题
若二阶常系数线性齐次微分方程y"+ay'+by=0的通解为y=(C1+C2x)e^x，则非齐次方程y"+ay'+by=x满足条件y(0)=2，y'(0)=0的解为y=________.
考题
单选题若二阶常系数线性齐次微分方程y″＋ay′＋by＝0的通解为y＝（C1＋C2x）ex，则非齐次方程y″＋ay′＋by＝x满足条件y（0）＝2，y′（0）＝0的解为y＝（ ）。A
xex＋x2＋2B
－xex＋x2＋2C
－xex＋x＋2D
－xex＋x
考题
单选题设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（ ）。A
y″－y′＋y＝0B
y″－2y′＋2y＝0C
y″－2y′＝0D
y′＋2y＝0
考题
单选题以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是（ ）。[2012年真题]A
y″-2y′-3y=0B
y″+2y′-3y=0C
y″-3y′+2y=0D
y″-2y′-3y=0
考题
单选题（2012）以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是：（）A
y″-2y′-3y=0B
y″+2y′-3y=0C
y″-3y′+2y=0D
y″+2y′+y=0
考题
单选题设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（ ）。A
y″＋2y′＋2y＝0B
y″－2y′＋2y＝0C
y″－2y′－2y＝0D
y″＋2y′＋2y＝0
热门标签
最新试卷