网友您好， 请在下方输入框内输入要搜索的题目：

2020人教版五年级数学下册全套单元测试题及答案

用棱长1cm的小正方体摆成稍大一些的正方体，至少需要多少个小正方体？动手摆摆看。

从系统的视角看,任何一种领导活动,一般都是由()基本要素构成。

A.4个

B.1个

C.3个

D.2个


正确答案：C

有两个相同的正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6。将两个正方体放在桌面上，向上的一面数字之和为偶数的有多少种情形?（ ）

A．9

B．12

C．18

D．24


正确答案：C
和为偶数有两种情况，一种是向上的两面都是奇数，另一种情况都是偶数，因此有N=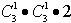=3×3×2=18。

有两个相同的正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6。将两个正方体放到桌面上，向上的一面数字之和为偶数的有多少种情形？（ ）

A.9

B.12

C.18

D.24

第一部分 数量关系（共25题，参考时限20分钟）

一、数字推理（本部分包括两种类型的题目，共10题。 ）

（一）每题给你一个数列，但其中缺少一项，要求你仔细观察数列的排列规律，然后从四个供选择的选项中选出你认为最合理的一项，来填补空缺项。 请开始答题：

1.6,7,3,0,3,3,6,9,5，( )

A.4

B.3

C.2

D.1


正确答案：A

-精选范文、公文、论文、和其他应用文档，如需本文，请下载- 2020 人教版五年级数学下册全套单元测试题及答案 第一单元过关检测卷 一、填空。 ( 每题 3 分，共 9 分) 1把一个魔方放在桌子上，从正面、上面、左面看到的都是( ) 。 2一个立体图形，从正面和上面看都是，从左面看是，则这个立体图形 是由( ) 个同样大小的正方体组成的。 3从同一个方向观察一个正方体最多能看到( )个面。 二、判断。 ( 每题 3 分，共 9 分) 1由相同个数的正方体摆成的物体从上面看的图形都是相同的。( ) 2由 3 个拼成一个物体，从正面看到的是，那么这 3 个只有 2 种 摆法。 ( ) 3 一 个 物体 从 左 面 看 到 的 是 ，这 个 物 体 不 一定 是 由4 个 正 方 体 摆 成 的 。 ( ) 三、选择。 ( 每题 3 分，共 18 分) 1如图，它是由6 个同样大小的正方体摆成的几何体。将正方体移走后，从正面、 上面和左面观察新几何体与从正面、上面和左面观察原几何体相比，下列说法正确 的是( )。 A从正面看到的图形没有发生改变 B 从上面看到的图形没有发生改变 -精选范文、公文、论文、和其他应用文档，如需本文，请下载- C从左面看到的图形没有发生改变 D 从任何一面看到的图形都发生了改变 2. 用 5 个同样大小的正方体摆一摆，要求从正面看到的是， 从左面 看到的是，从上面看到的是。下面的摆法中， ( ) 符合要求。 A B. C. D. 3用 5 个同样大小的正方体搭成一个立体图形，从正面看是，从上面看 是，从右面看是，这个立体图形是 ( ) 。 A B. C. D. 4给左边的立体图形添一个，使得从上面看到的形状如右图，摆法正确的是 ( )。 A B C D 5一个立体图形由6 个同样大小的正方体组成，从左面看形状是，从上面看 形状是，共有 ( )种不同的搭法。 A3 B6 C7 D8 6如图所示，是由几个相同小正方体搭成的几何体从上面看到的图形，小正方形内的 -精选范文、公文、论文、和其他应用文档，如需本文，请下载- 数字表示在该位置的小正方体的个数。则这个几何体从前面看是( ) ，从右面看 是( )。 A B C D 四、用同样大的正方体摆成下面的几个物体。(每空 3 分，共 18 分) 1从正面和左面看都是的有( )。 2( ) 和( ) 从上面看是。 3从正面看 ( ) 和从上面看 ( )都是。 4 如果从正面看到的和一样， 用 5 个正方体摆，摆成两行，有( )种不同的摆法。 五、如图是由几个同样的小正方体所组成的几何体从上面看到的图形，小正方形中的 数字表示在该位置的小正方体的个数，在下列方格图中画出从正面和左面看到的图 形。 (10 分) 从正面看从左面看 六、按从不同方向看到的形状，搭一个用5 个小正方体组成的立体图形。(1 题 6 分，2 题 8 分，共 14 分) -精选范文、公文、论文、和其他应用文档，如需本文，请下载- 从上面看从正面看 1它可能是下面的哪一个呢？对的在( ) 内打“”，不对的在 ( ) 内打“”。 ( ) ( ) 2你能找到几种不同的搭法？分别画出从左面看到的形状。 七、一个几何体，从正面看到的图形是，我们可以初步判断这个几何体最 少由( )个小正方体组成， 如果它是从由 6 个小正方体组成的几何体的正面看到 的图形，该几何体只有两行，有( )种不同的摆法。 (8 分) 八、数一数。 (8 分) ( )个 ( )个 九、根据从不同方向看到的三个图形说出拼摆这个立体图形用了几个小正方体。(6 分) 从正面看从左面看从上面看 -精选范文、公文、论文、和其他应用文档，如需本文，请下载- 答案 一、1正方形26 33 二、12 3 三、1.C 2.B 3.C 4.B 5.A 6.B C 四、1. 2. 3. 4. 16 五、 从正面看从左面看 六、1. 22 种 七、5 20 八、10 16 九、8 个 -精选范文、公文、论文、和其他应用文档，如需本文，请下载- 第二单元过关检测卷 一、我会填。 ( 每空 1 分，共 35分) 112 的因数有 ( )，50 以内 15的倍数有 ( )。 2三位数中，最大的奇数是( )，最大的偶数是 ( )。 3一个合数至少有 ( ) 个因数，一个质数只有 ( )个因数。 438 至少加 ( )是 3 的倍数，至少减 ( )是 5 的倍数。 5一个数的因数的个数是( ) ，其中最小的因数是( ) ，最大的因数是 ( )；一个数的倍数的个数是( )，最小的倍数是 ( )。 6 在 17， 6， 13， 9， 2， 34， 1， 48， 39 中， 奇数有( )， 偶数有( )， 质数有 ( ) ，合数有 ( ) 。 7两个连续的偶数的和的平均数是19，这两个偶数分别是 ( )和( )。 8用质数填空，所用的质数不能重复。 26( )( )( )( )( ) ( ) 9同时是 2，3，5 三个数的倍数的最大两位数是( )，最小三位数是 ( )。 10按要求在里填上最小的数字。 (1)26 (2和 3 的倍数 ) (2)183 (2和 5 的倍数 ) (3)30 5(3和 5 的倍数 ) (4)7 90(2，3 和 5 的倍数) (5)23 45( 和是奇数 )

：有两个相同的正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6。将两个正方体放到桌面上，向上的一面数字之和为偶数的有多少种情形?（ ）。

A．9

B．12

C．18

D．24


正确答案：C

（a）从结构上可将城域网分成如图2-1所示①、②和③共3个层次，写出这3个层次的名称。（3分）

（b）用户接入到城域网中的方式是ADSL，用户主机与BRAS间使用的协议是什么？ (1分）


正确答案：
（a）①接入层②汇聚层③核心层
（b）用户接入到城域网中的方式是ADSL，用户主机与BRAS间使用的协议是PPPoE。

一个木制正方体在表面涂上颜色，将它的每条棱三等分，然后从等分点将正方体展开，得到27个小正方体，将这些小正方体充分混合后，装入一个口袋，从这个口袋中随机取出两个小正方体，其中一个正方体只有一个面涂有颜色，另一个只有2个面涂有颜色的概率约为（ ）

A. 0.05
B. 0.17
C. 0.34
D. 0.67

答案：C
解析：
涂一面的6个 涂2面的12个 满足条件情况72个，经计算为0.34

如下图所示，一个小正方体的表面积为64平方厘米，则几何物体甲垒放成几何物体乙后，物体甲与物体乙表面积之比为：

A.3∶2
B.4∶3
C.8∶7
D.9∶8

答案：D
解析：
第一步，本题考查几何问题，属于立体几何类。
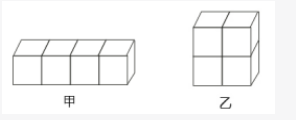
第二步，甲和乙都是由相同的4个小正方体组成，由图可知，几何物体甲的表面积一共包含了18个面，而几何物体乙包含了16个面，所以甲与乙表面积之比为18∶16＝9∶8。

如下图所示，一个小正方体的表面积为64平方厘米，则几何物体甲垒放成几何物体乙后，物体甲与物体乙表面积之比为：

A.3∶2
B.4∶3
C.8∶7
D.9∶8

答案：D
解析：
第一步，本题考查几何问题，属于立体几何类。
第二步，甲和乙都是由相同的4个小正方体组成，由图可知，几何物体甲的表面积一共包含了18个面，而几何物体乙包含了16个面，所以甲与乙表面积之比为18∶16＝9∶8。

更多 “2020人教版五年级数学下册全套单元测试题及答案” 相关考题
考题 下图是从不同角度观察同一个正方体得到的图像，该正方体的六个面分别被标记为1到6，则不可能相对的两个面是（ ）。 A.1和6 B.2和5 C.3和4 D.4和5答案：D解析：第一步，明确提问方式。 从不同角度观察同一个正方体得到的图像，该正方体的六个面分别被标记为1到6，选择不可能是相对的两个面。 第二步，找规律。 根据题干可知，两个图中都出现了面2，面2的相邻面分别是1、3、6，根据六面体面之间的关系，可知面4或者面5与面2为相对面，那么面4和面5就不能是彼此的相对面。 因此，选择D选项。
查看答案
考题 一个由若干个单位立方体组成的立体图形，从正面看、左侧面看、下面看都是一个3*3的正方形，那么这个立体图形至少需要_________个单位立方体。A.17 B.19 C.21 D.22答案：A解析：题干要求从正面、左侧面、下面看均为3×3的正方形，先在下面平铺一层，共 9 个立方体；接下来满足正面和左侧面，只需要 6 个立方体即可。如下图所示，共有9+6=15个立方体。所以至少需要 15 个单位立方体。
查看答案
考题 一个大的正方体的6个面分别写有数字1~6，甲乙丙丁四人分别面对正方体的四个侧面，分别能看到正方体的一个侧面和顶部。甲乙丙三人看到的正方体侧面和顶部的点数之和分别是4、9和5。则正方体底部的点数是（ ）。A.4或5 B.3或4 C.2或3 D.1或2答案：A解析：第一步，本题考查其他几何类。 第二步，由于甲乙丙三人看到的均是侧面+顶面，甲乙点数之差为9－4=5，乙丙点数之差为9－5=4，在1—6这个6个点数之中，1与6相差为5，6与2相差为4，故甲乙丙看到侧面上的点数依次为1、6、2，则顶面点数必为3。故底部的点数只能是4或5。
查看答案
考题 把若干个大小相同的水立方摆成如图形状！从上向下数，摆1层有1个立方体，摆2层共有4个立方体，摆3层共有10个立方体，问摆7层共有多少个立方体？ A. 60 B. 64 C. 80 D. 84答案：D解析：数量问题，根据规律得出数列：1+3+6+10+15+21+28=84
查看答案
考题 一个大的正方体的6个面分别写有数字1~6，甲乙丙丁四人分别面对正方体的四个侧面，分别能看到正方体的一个侧面和顶部。甲乙丙三人看到的正方体侧面和顶部的点数之和分别是4、9和5。则正方体底部的点数是（ ）。A.4或5 B.3或4 C.2或3 D.1或2答案：A解析：第一步，本题考查其他几何类。 第二步，由于甲乙丙三人看到的均是侧面+顶面，甲乙点数之差为9－4=5，乙丙点数之差为9－5=4，在1—6这个6个点数之中，1与6相差为5，6与2相差为4，故甲乙丙看到侧面上的点数依次为1、6、2，则顶面点数必为3。故底部的点数只能是4或5。
查看答案
考题 下图是从不同角度观察同一个正方体得到的图像，该正方体的六个面分别被标记为1到6，则不可能相对的两个面是（ ）。 A.1和6 B.2和5 C.3和4 D.4和5答案：D解析：第一步，明确提问方式。 从不同角度观察同一个正方体得到的图像，该正方体的六个面分别被标记为1到6，选择不可能是相对的两个面。 第二步，找规律。 根据题干可知，两个图中都出现了面2，面2的相邻面分别是1、3、6，根据六面体面之间的关系，可知面4或者面5与面2为相对面，那么面4和面5就不能是彼此的相对面。 因此，选择D选项。
查看答案
考题 一个由若干个单位立方体组成的立体图形，从正面看、左侧面看、下面看都是一个3X3的正方形，那么这个立体图形至少需要______个单位立方体。A.17 B.19 C.21 D.22答案：A解析：题干要求从正面、左侧面、下面看均为3X3的正方形，先在下面平铺- -层，共9个立方体;接下来满足正面和左侧面，只需要6个立方体即可。如下图所示，共有9+6= 15个立方体。所以至少需要15个单位立方体。
查看答案
考题 一个木制正方体在表面涂上颜色，将它的每条棱三等分，然后从等分点将正方体展开，得到27个小正方体，将这些小正方体充分混合后，装入一个口袋，从这个口袋中随机取出两个小正方体，其中一个正方体只有一个面涂有颜色，另一个只有2个面涂有颜色的概率约为（ ）A. 0.05 B. 0.17 C. 0.34 D. 0.67答案：C解析：涂一面的6个 涂2面的12个 满足条件情况72个，经计算为0.34
查看答案
考题 把如干个大小相同的立方体摆成如图形状：从上向下数，摆1层有一个立方体，摆2层共有4个立方体，摆3层共有10个立方体，问摆7层共有多少个立方体？ A. 60 B. 64 C. 80 D. 84答案：D解析：依题，第一层开始，依次往下每层数量分别为1、3、6、10、15、21、28，七层总和为84个。
查看答案
考题 有两个相同的正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6。将两个正方体放到桌面上，向上的一面数字之和为偶数的有多少种情形？（ ）。A．9 B．12 C．18 D．24答案：C解析：和为偶数有两种情况，一种是向上的两面均为偶数，一种是都为奇数。因此，有N= C13?C13?2=s3×3×2=18。
查看答案
热门标签
最新考题
最新试卷
热门试卷