网友您好, 请在下方输入框内输入要搜索的题目:
一、考题回顾


【教学过程】
(一)导入新知
教师:同学们,大约一千五百多年前,我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
出示主题图:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?

教师:从题中获取信息,你知道了什么,要求什么问题?
(二)讲解新知
1.尝试解决,交流想法。
问题:同学们想一想,算一算鸡和兔各有多少只?
2.感受化繁为简的必要性。
大家在刚才猜了好几组数据,经过验证都不正确,为什么猜不对呢?
例1.“笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?”
教师:从题中你们能获取哪些信息?和生活常识联系在一起,你还能说出哪些信息?
3.猜想验证。
教师:有了这些信息,我们先来猜猜,笼子可能会有几只鸡?几只兔?猜测需要抓住哪个条件?
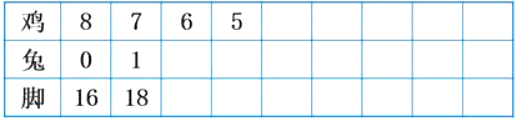
学生汇报。
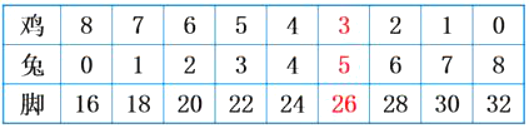
小结:这个方法挺好,能帮我们解决鸡兔同笼的问题,我们把这种方法叫做列表法。(板书:列表法)
小组讨论上表中数量之间一些数学规律,汇报。
4.数形结合理解假设法。
(1)假设全是鸡。
教师:我们先看表格中左起的第一列,8和0是什么意思?

(2)假设全是兔。
教师:我们再回到表格中,看看右起第一列中的0和8是什么意思?

(3)提出假设法概念。
刚才我们通过假设都是鸡或都是兔来解决例1的,所以把这种方法叫做假设法。这是解决“鸡兔同笼”问题的一种基本方法,也是算术方法中较为普遍的一般方法。
(板书:假设法)
(三)应用新知
利用两种方法解决古代数学问题:
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
(四)小结作业
小结:总结解决古代著名的“鸡兔同笼”问题的两种方法(列表法和假设法)
作业:课后查阅数学名著《孙子算经》,找一找其他相关的数学问题,试着解决问题。
【板书设计】
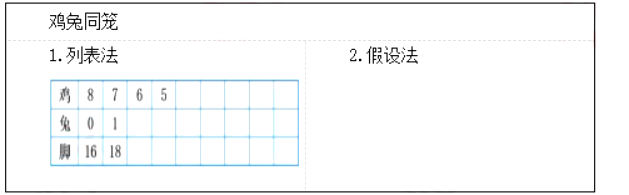
【答辩题目解析】
1.解决鸡兔同笼问题有哪些方法?
【参考答案】
列表法;假设法,分为假设全是鸡和假设全是兔子两种情况;以及方程法等.
2.你的课堂中哪个环节体现了学生的独立思考?
【参考答案】
在新课导入部分,引导学生思考理解题干的含义,培养学生的独立思考的能力;在新课部分,设置小组交流,培养学生的合作交流和独立思考的能力,感受列表法的一般性和注意事项。其次在应用新知部分,引导学生独立自主解决问题,体现了学生的独立思考。
鸡兔同笼问题若是转化为数学应用题,可以使用数学的()来解决。
- A、求最大值方法
- B、四舍五入方法
- C、解方程组法
- D、比较大小法
正确答案:C
展示是对导学案上问题答案的重复性讲解。
正确答案:错误
教科书问题解决中,对例题的作用叙述不正确的是()
- A、当学生能够识别出新的问题与例题之间的相似性后,他就可以将例题的解题程序迁移到新的问题中
- B、例题对于学生解决新的问题作用很小
- C、例题则可以为学生提供一个如何将原理应用到实际问题的典型范例
- D、通过学习例题,学生可以学会特定的操作步骤和程序
正确答案:B
复合应用题教学的中心环节是()。
- A、解析应用题
- B、列出方程
- C、解答应用题
- D、检验答案
正确答案:A
鸡兔同笼问题假设笼子里全部都是鸡,每只鸡有2只脚,那么一共应该有35×2=70(只)脚,而实际有94只脚,这多出来的脚就是把兔子当作鸡多出来的,每只兔子比鸡多2只脚,一共多了94-70=24(只),则兔子有24÷2=12(只),那么鸡有35-12=23(只)。解:假设全部都是鸵鸟,则一共有70×2=140(只)脚,此时长颈鹿的脚数是0,鸵鸟脚比长颈鹿脚多140只,而实际上鸵鸟的脚比长颈鹿多80只,因此鸵鸟脚与长颈鹿脚的差数多了140-80=60(只),这是因为把其中的长颈鹿换成了鸵鸟。把每一只长颈鹿换成鸵鸟,鸵鸟的脚数将增加2只,长颈鹿的脚数减少4只,那么鸵鸟脚数与长颈鹿脚数的差就增加了6只,所以换成鸵鸟的长颈鹿有60÷6=10(只),鸵鸟有70-10=60(只)。解:根据题意可得:前后鸡的总只数=前后兔的总只数。把1只鸡和1只兔子看做一组,共有6条腿。前后鸡和兔的总腿数有144+156=300(条),所以共有300÷6=50(组),也就是鸡和兔的总只数有50只。
教学设计题: 请认真阅读下述材料,并按要求作答。 《孙子算经》中有一道非常有名的题目"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"请根据给出例题设计鸡兔同笼问题的讲解:今有鸡兔同笼,上有一十二头,下有三十足,问鸡兔各几何? 试分析鸡兔同笼问题的解题规律。
正确答案:解答鸡兔问题一般采用假设法,假设全是一种动物(如全是"鸡"或全是"兔",然后根据出现的腿数差,可推算出某一种的头数。
解题规律:(总腿数-鸡腿数×总头数)÷一只鸡兔腿数的差=兔子只数
兔子只数=(总腿数-2×总头数)÷2
如果假设全是兔子,则有:鸡的只数=(4×总头数-总腿数)-2;兔的头数=总头数-鸡的只数。
教学设计题: 请认真阅读下述材料,并按要求作答。 《孙子算经》中有一道非常有名的题目"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"请根据给出例题设计鸡兔同笼问题的讲解:今有鸡兔同笼,上有一十二头,下有三十足,问鸡兔各几何? 如指导高年级小学生学习,试确定教学目标和教学重点。
正确答案:教学目标:
①知识与技能目标:了解"鸡兔同笼"问题,尝试用不同的方法解决"鸡兔同笼"问题,使学生体会假设和列方程的一般性。
②过程与方法目标:通过不同方法的对比,培养学生的发散思维能力,并向学生渗透转化的思想。
③情感态度与价值观目标:感受古代数学问题的趣味性,培养学生热爱祖国文化的感情。
教学重点:用不同的方法解决"鸡兔同笼"问题。
教学设计题: 请认真阅读下述材料,并按要求作答。 《孙子算经》中有一道非常有名的题目"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"请根据给出例题设计鸡兔同笼问题的讲解:今有鸡兔同笼,上有一十二头,下有三十足,问鸡兔各几何? 试分析鸡兔同笼问题的解题规律。
正确答案:解答鸡兔问题一般采用假设法,假设全是一种动物(如全是"鸡"或全是"兔",然后根据出现的腿数差,可推算出某一种的头数。
解题规律:(总腿数-鸡腿数×总头数)÷一只鸡兔腿数的差=兔子只数
兔子只数=(总腿数-2×总头数)÷2
如果假设全是兔子,则有:鸡的只数=(4×总头数-总腿数)-2;兔的头数=总头数-鸡的只数。
教学设计题: 请认真阅读下述材料,并按要求作答。 《孙子算经》中有一道非常有名的题目"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"请根据给出例题设计鸡兔同笼问题的讲解:今有鸡兔同笼,上有一十二头,下有三十足,问鸡兔各几何? 如指导高年级小学生学习,试确定教学目标和教学重点。
正确答案:教学目标:
①知识与技能目标:了解"鸡兔同笼"问题,尝试用不同的方法解决"鸡兔同笼"问题,使学生体会假设和列方程的一般性。
②过程与方法目标:通过不同方法的对比,培养学生的发散思维能力,并向学生渗透转化的思想。
③情感态度与价值观目标:感受古代数学问题的趣味性,培养学生热爱祖国文化的感情。
教学重点:用不同的方法解决"鸡兔同笼"问题。
教学设计题: 请认真阅读下述材料,并按要求作答。 《孙子算经》中有一道非常有名的题目"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"请根据给出例题设计鸡兔同笼问题的讲解:今有鸡兔同笼,上有一十二头,下有三十足,问鸡兔各几何? 如指导高年级小学生学习,试确定教学目标和教学重点。
正确答案: 教学目标:
①知识与技能目标:了解"鸡兔同笼"问题,尝试用不同的方法解决"鸡兔同笼"问题,使学生体会假设和列方程的一般性。
②过程与方法目标:通过不同方法的对比,培养学生的发散思维能力,并向学生渗透转化的思想。
③情感态度与价值观目标:感受古代数学问题的趣味性,培养学生热爱祖国文化的感情。
教学重点:用不同的方法解决"鸡兔同笼"问题。
更多 “小学典型应用题18:鸡兔同笼问题(例题 视频讲解 答案)” 相关考题
- 三国两晋南北朝时期纳礼入律的典型代表是()。A、八议入律B、确立重罪十恶C、官当入律D、服制入律
- 对交通违法行为事实清楚,处以暂扣机动车驾驶证的,应当自违法行为人接受处理之日起()作出处罚决定。A、二十四小时内B、二日内C、三日内D、七日内
- 违反道路交通安全法律、法规,发生重大交通事故后逃逸,构成犯罪的,由公安机关交通管理部门吊销机动车驾驶证,且()不得重新取得机动车驾驶证。A、二年内B、三年内C、五年内D、终生
- 国家实行机动车()强制保险制度,设立道路交通事故社会救助基金。A、车辆损失险B、第三者责任C、全车盗抢D、车上人员责任险
- 剪刀机设备不得随意改动,安全防护设施不得任意()
- 利用WinRAR,可以在压缩文件(夹)过程中设置密码,其过程包括:()A、右键单击要加密的文件(夹),选择“添加到压缩文件”B、选择“高级”选项卡,选择“设置密码”C、两次输入密码后,选择“加密文件名”D、单击“确定”
- 精炼炉工作之前,应检查确保设备处于良好待机状态、各介质参数符合要求
- 在轧钢车间内行走或作业时可由以下方式进入生产岗位或通行:()A、安全过桥B、安全通道C、跨越辊道上方D、穿越设备下方
- 2011年5月13日,张某(持C1证)驾驶自己的轿车,与同方向在前李某驾驶的二轮摩托车相撞,致李某与当场死亡,张某当场报案并在现场等候交警处理。后经民警调查,事故因张某醉酒后驾驶机动车造成,负事故的全部责任。公安机关应当对张某怎样处理?如果追刑应当以什么罪名立案?
- 只要空气与煤气混合,遇明火就会发生爆炸。