网友您好, 请在下方输入框内输入要搜索的题目:
已知公比为q的等比数列{an)中,a2=4,a5=-32.
(I)求q;
(11)求{an}的前6项和S6.
q=-2.
A、权数以公差为1的等差数列
D、权数以公比为2的
C、权数逐渐递减
B、权数逐渐递增等比数列
设Sn为等差数列{an}的前n项和,若S3=3,S6=24,则a9= 。
15
B.2
C.-3
D.4

B.必要不充分条件
C.充要条件
D.既不充分也不必要条件

9答案:A2020全国卷真题分类数列1、(2020卷一理17)设a是公比不为1的等比数列,a为a,a的等差中项.n123(1)求a的公比;n若ai1,求数列na的前n项和.答案:1)故a的公比为2.n2)S-1-(3n+1)(2)nn92、(2020卷文10).设a是等比数列,且a+a+a1,a+a+a2,则a+a+an123234678A12B24C30D32答案:D3、(2020卷一文16).数列a满足a.+(1)na3n1,前16项和为540,则na1答案:74、(2020卷二理6).数列a中,a2n1aa.若am+nmnk+1+a+a21525k+2k+10A2B3C4D5答案:C5、(2020卷二文3).如图,将钢琴上的L2个键依次记为ai,a2,:ai2.设1wij0cos2a0sin2a0答案:D4、贝cos2x=(2020卷二文13)若sinx二扌,1答案:9n5、(2020卷三理9).已知2tanO-tan(0+-)=7,则tanO=A.-2B.-1C.1D.2答案:D16、(2020卷三理16)关于函数f(x)二sinx+一有如下四个命题:sinxf(x)的图像关于y轴对称f(x)的图像关于原点对称.冗f(x)的图像关于直线x二2对称f(x)的最小值为2.其中所有真命题的序号是答案:nn7、(2020卷三文5)已知sin9+sin(9+)=1,则sin(9+)=36A1B.主3C2D.叵答案:B2332三、解三角形1、(2020卷一文18)ABC的内角A,B,C的对边分别为a,b,c已知B=150若a二3c,b=2、7,求ABC的面积;(2)若sinA+sinC=,求C.2答案:(1)V3C=152、(2020卷二理17)abc中,sin2Asin2Bsin2C二sinBsinC.(1)求A;(2)若BC=3,求ABC周长的最大值.2nl答案:(1)A=-3(2)3+233、(2020卷二文17)ABC的内角A,B,C的对边分别为a,b,c,已知cos2(2+A)+cosA=4.J3(1)求A;(2)若bc=计a,证明:ABC是直角三角形.24、(2
B.45
C.42
D.36
 两式相减得到a1 =3,因此数列前四项之和为3×(24-1)=45.
两式相减得到a1 =3,因此数列前四项之和为3×(24-1)=45.
B.85
C.80
D.75
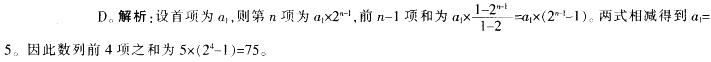
(Ⅰ)设bn=an+1-2an,求证:数列{bn)是等比数列;
(Ⅱ)设
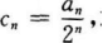 求证:数列{cn}是等差数列;
求证:数列{cn}是等差数列;
(Ⅲ)求数列{an}的通项公式及前n项和.

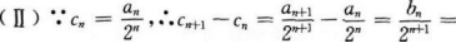


B.85
C.80
D.75

更多 “2020全国卷真题分类(数列、三角、解三角形、立体几何)20220728.docx” 相关考题
- 根据奥尔德佛的ERG理论,人的核心需要包括( ). A.成就需求 B。生存需要 C。关系需要 D.权力需要 E.成长需要
- 下面观点哪个更符合社会学习理论的人格观( )。A.人格是受个人本能驱动的B.人格是人与环境相互作用的结果C.人格是外显与内隐反应的总和,这些反应是个人被强化后的结果D.人格是外在环境塑造的产物
- ( 难度:中等)Hive与传统关系型数据库对比,优势有A.计算能力更强B.延迟更低C.扩展性更好D.索引各类更多
- 对贷款逾期期间不能按期归还的利息,按规定计收复利。
- 1980年中国的GDP是美国的____,到2020年中国的GDP是美国的____?
- 美国在冷战之后进行了三次大的战略调整,第一次克林顿政府提出了什么?下列选项错误的是A.“全球反恐战争B.“亚太再平衡C.“称霸战争D.“参与和扩展战略
- 小张毕业后进入了一家广告公司,凭着过硬的专业素质和不懈的努力很快成为公司的业务骨干,并被提拔为部门经理。但让公司领导略感意外的是,小张升为主管后虽然依然工作勤恳,但他所管理的部门的整体业绩反而较先前有所下降。通过私下询问,员工们普遍反映小张对下属缺乏适当的管理和激励,他似乎并不关心下属的工作绩效问题。问题一:从小张的表现可以看出,他具有较高的( )。 A.亲和需要 B.安全需要 C。权力需要 D.成就需要问题二:具有小张这种较高需要的入,通常有以下特点( )。 A.责任感较弱 B。希望别人顺从自己的意志 C。喜欢得到及时的反馈情况 D.经常选择做有适度风险的工作问题三:根据麦克里兰提出的需要理论,亲和需求高的人常常( )。A。不易受他人影响 B。在组织中充当管理者的角色 C。看重能否被他人接受 D.喜欢能体现其地位的场合
- 借贷记账法的主要内容是什么?
- ( 难度:中等)关于hive的说法正确的是A.增加map和reduce数量可以提高计算速度,因此数量越多越好B.为了提高速度可以开启小文件本地化执行C.压缩可以减小文件体积,因此压缩率越大的算法越好D.每个查询被Hive转化为多个阶段,有些阶段关联性不大,则可以并行化执行,减少执行时间
- 中长期贷款展期不得超过原贷款期限的一半,最长不得超过5年.
- 2022年怀化市通道侗族自治县妇幼保健院医护人员招聘模拟试题及答案解析-
- 2022年张家界市慈利县妇幼保健院医护人员招聘考试题库及答案解析-
- 2022年张家口市尚义县妇幼保健院医护人员招聘考试题库及答案解析-
- 2022年延安市子长县妇幼保健院医护人员招聘考试题库及答案解析-
- 2022年常德津市市妇幼保健院医护人员招聘题库及答案解析-
- 2022年巴中市南江县妇幼保健院医护人员招聘考试题库及答案解析-
- 2022年双鸭山市妇幼保健院医护人员招聘模拟试题及答案解析-
- 2022年南阳市桐柏县妇幼保健院医护人员招聘模拟试题及答案解析-
- 2022年兰州市城关区妇幼保健院医护人员招聘模拟试题及答案解析-
- 2022年信阳市息县妇幼保健院医护人员招聘模拟试题及答案解析-