网友您好, 请在下方输入框内输入要搜索的题目:
【题目描述】
第4题:
正确答案:A
( 98~100 题共用备选答案)

第 98 题 与消化性溃疡的发病有关( )
【题目描述】
第1题:
|
正确答案:A |
答案分析:

【题目描述】
第20题:
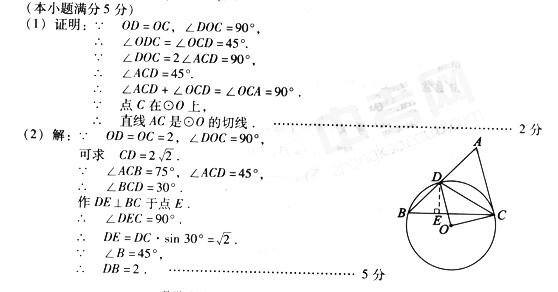
( 99~100 题共用备选答案)
第 99 题 休克代偿期病人表现为( )

2010年中考数学压轴题100题精选(1-10题)答案【001】解:(1) 抛物线 经过点 ,········································································ 1分二次函数的解析式为: ········································ 3分(2) 为抛物线的顶点 过 作 于 ,则 ,········································· 4分当 时,四边形 是平行四边形······································· 5分当 时,四边形 是直角梯形过 作 于 , 则(如果没求出 可由 求 )·········································································· 6分当 时,四边形 是等腰梯形综上所述:当 、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形.· 7分(3)由(2)及已知, 是等边三角形则过 作 于 ,则 ·························································· 8分= ·························· 9分当 时, 的面积最小值为 ····················································· 10分此时【002】解:(1)1, ;(2)作QF⊥AC于点F,如图3, AQ = CP= t,∴ .得 .∴ . ∴ ,即 .(3)能.∵DE⊥PQ,∴PQ⊥QB,四边形QBED是直角梯形.此时∠AQP=90°.由△APQ∽△ABC,得 ,即 . 解得 .②如图5,当PQ∥BC时,DE⊥BC,四边形QBED是直角梯形.此时∠APQ =90°.由△AQP∽△ABC,得 ,即 . 解得 .(4) 或 .【注:①点P由C向A运动,DE经过点C.方法一、连接QC,作QG⊥BC于点G,如图6., .由 ,得 ,解得 .方法二、由 ,得 ,进而可得,得 ,∴ .∴ .②点P由A向C运动,DE经过点C,如图7., 】【003】解.(1)点A的坐标为(4,8) …………………1分将A (4,8)、C(8,0)两点坐标分别代入y=ax2+bx8=16a+4b得0=64a+8b解 得a=- ,b=4∴抛物线的解析式为:y=- x2+4x …………………3分(2)①在Rt△APE和Rt△ABC中,tan∠PAE= = ,即 =∴PE= AP= t.PB=8-t.∴点E的坐标为(4+ t,8-t).∴点G的纵坐标为:- (4+ t)2+4(4+ t)=- t2+8. …………………5分∴EG=- t2+8-(8-t) =- t2+t.∵- <0,∴当t=4时,线段EG最长为2. …………………7分②共有三个时刻. …………………8分t1= , t2= ,t3= . …………………11分【004】(1)解:由 得 点坐标为由 得 点坐标为 ∴ (2分)由 解得 ∴ 点的坐标为 (3分)∴ (4分)(2)解:∵点 在 上且 ∴ 点坐标为 (5分)又∵点 在 上且 ∴ 点坐标为 (6分)∴ (7分)(3)解法一: 当 时,如图1,矩形 与 重叠部分为五边形 ( 时,为四边形 ).过 作 于 ,则∴ 即 ∴∴即 (10分)∵ 为 的中点,∴在 中, ∴ ··········· 2分∴即点 到 的距离为 ·································· 3分(2)①当点 在线段 上运动时, 的形状不发生改变.∵ ∴∵ ∴ ,同理 ············································································ 4分如图2,过点 作 于 ,∵∴∴则在 中,∴ 的周长= ···································· 6分②当点 在线段 上运动时, 的形状发生改变,但 恒为等边三角形.当 时,如图3,作 于 ,则类似①,∴ ············································································· 7分∵ 是等边三角形,∴此时, ································· 8分此时,当 时,如图5,则 又∴因此点 与 重合, 为直角三角形.∴此时,综上所述,当 或4或 时, 为等腰三角形.【006】解:(1)OC=1,所以,q=-1,又由面积知0.5OC×AB= ,得AB= ,设A(a,0),B(b,0)AB=b-a= = ,解得p= ,但p0,所以p= 。所以解析式为:(2)令y=0,解方程得 ,得 ,所以A( ,0),B(2,0),在直角三角形AOC中可求得AC= ,同样可求得BC= ,显然AC2+BC2=AB2,得△ABC是直角三角形。AB为斜边,所以外接圆的直径为AB= ,所以 。(3)存在,AC⊥BC,①若以AC为底边,则BD//AC,易求AC的解析式为y=-2x-1,可设BD的解析式为y=-2x+b,把B(2,0)代入得BD解析式为y=-2x+4,解方程组 得D( ,9)②若以BC为底边,则BC//AD,易求BC的解析式为y=0.5x-1,可设AD的解析式为y=0.5x+b,把 A( ,0)代入得AD解析式为y=0.5x+0.25,解方程组 得D( ) 综上,所以存在两点:( ,9)或( )。【007】【008】证明:(1)∵∠ABC=90°,BD⊥EC,∴∠1与∠3互余,∠2与∠3互余,∴∠1=∠2…………………………………………………1分∵∠ABC=∠DAB=90°,AB=AC∴△BAD≌△CBE…………………………………………2分∴AD=BE……………………………………………………3分(2)∵E是AB中点,∴EB=EA由(1)AD=BE得:AE=AD……………………………5分∵AD∥BC∴∠7=∠ACB=45°∵∠6=45°∴∠6=∠7由等腰三角形的性质,得:EM=MD,AM⊥DE。即,AC是线段ED的垂直平分线。……………………7分(3)△DBC是等腰三角(CD=BD)……………………8分理由如下:由(2)得:CD=CE由(1)得:CE=BD∴CD=BD∴△DBC是等腰三角形。……………………………10分【009】四边形 为矩形.轴, 轴,四边形 为矩形.轴, 轴,四边形 均为矩形.········· 1分,,..,,.··········································································· 2分②由(1)知 ...······················································································ 4分,.············································································· 5分..······················································································· 6分轴,四边形 是平行四边形..······················································································· 7分同理 ..······················································································· 8分(2) 与 仍然相等.······································································· 9分,又 ,.·························· 10分..,...······················································································ 11分轴,四边形 是平行四边形..同理 ..····················································································· 12分【010】解得 抛物线对应的函数表达式为 . 3分(2)存在.在 中,令 ,得 .令 ,得 , ., , .又 , 顶点 .························································· 5分容易求得直线 的表达式是 .在 中,令 ,得 ., .·········································································· 6分在 中,令 ,得 .., 四边形 为平行四边形,此时 .··························· 8分(3) 是等腰直角三角形.理由:在 中,令 ,得 ,令 ,得 .直线 与坐标轴的交点是 , ., .································································· 9分又 点 , . .········································ 10分由图知 , .································· 11分,且 . 是等腰直角三角形.·························· 12分(4)当点 是直线 上任意一点时,(3)中的结论成立. 14分
( 99~100 题共用备选答案)
第 99 题 肋骨骨折应( )

根据以下答案请回答 98~100 题:
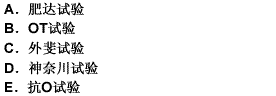
第 98 题 协助诊断肠热症选用
用已知伤寒、副伤寒沙门菌的O、H抗原检测受检血清中有无相应抗体的半定量凝集试验称肥达反应(Widaltest)。本试验能辅助诊断伤寒、甲、乙、丙型副伤寒沙门菌引起的肠热症。
100~101 题共用备选答案:

第 100 题 丙硫氧嘧啶( )。
100~102 题共用备选答案:

第 100 题 变异型心绞痛时宜选用( )。
【题目描述】
第5题:
|
正确答案:B |
答案分析:

更多 “2010年中考数学压轴题100题精选(110题)答案” 相关考题
- 模型材料包括()A、普通石膏B、硬质石膏C、超硬石膏D、嵌体蜡E、以上都对
- 问答题试述博士生导师遴选条件。
- 下列关于一指禅推法的叙述中,错误的是()A、以拇指端或螺纹面着力B、腕关节做主动摆动C、紧推慢移D、掌虚指实
- 商品会计软件与专用软件相结合,即具有购买软件的费用省.先进.实用等优势.又可弥补()的缺陷。A、费时B、不能充分满足管理需要C、费力D、不能申请评审
- 属于猪苓汤证的是()A、虚烦不得眠,反复颠倒,心中懊B、少阴病,得之二三日以上,心中烦,不得卧C、六七日不大便,烦不解,腹满痛D、少阴病,欲吐不吐,心烦,但欲寐E、少阴病,下利六七日,咳而呕渴,心烦不得眠
- 会计报表子系统与其他子系统相比,具有()特点。A、输入数据量少B、不设置报表数据直接修改功能C、输出信息的规定性强D、通用性更强、适用面更广E、图表并用进行报表分析
- 多选题临床带教通常有以下哪几种形式()A床旁示教B门诊示教C模仿示教D病例讨论E电子教材
- 女性,33岁,因牙齿松动就诊。检查:多数牙齿松动、移位,牙周袋探诊深度5~8mm。怀疑为侵袭性牙周炎,诊断前最为重要的辅助检查是()A、拍摄X线片B、咬合检查C、家族史D、细菌学检查E、白细胞趋化功能检查
- 对于焊件接触面要求,下列叙述哪项是错误的()A、点接触B、面接触C、相接面有一定粗糙度D、相接面缝隙小,一般为0.1~0.15mmE、相接面要清洁
- 当内生肌酐清除率(Ccr)为19~10ml/min,肾功能分期是()A、肾功能正常B、肾衰竭代偿期C、肾衰竭失代偿期D、肾衰竭期E、肾衰竭终末期