网友您好, 请在下方输入框内输入要搜索的题目:
A.对称矩阵
B.可逆矩阵
C.n阶矩阵的转置矩阵
D.线性方程组的系数矩阵
ICD-9-CM-3各章的分类轴心是( )。
A、操作类型
B、损伤部位
C、疾病性质
D、解剖系统
E、解剖系统和操作
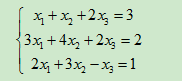
用初等变换的方法求解上述线性方程组。
答案:

第二部分矩阵本章概述矩阵是线性代数的重要内容,也是研究线性方程组和其它各章的主要工具。主要讨论矩阵的各种运算的概念和性质。在自学考试中,所占比例是各章之最。按考试大纲的规定,第二章占26分左右。而由于第三,四,五,六各章的讨论中都必须以矩阵作为主要工具,故加上试题中必须应用矩阵运算解决的题目的比例就要占到50分以上了。以改版后的三次考试为例,看下表按考试大纲所占分数07.407.707.10直接考矩阵这一章的26分左右31分34分38分加上其它章中必须用矩阵运算的所占分数51分53分67分由此矩阵这一章的重要性可见一般。2.1线性方程组和矩阵的定义2.1.1线性方程组n元线性方程组的一般形式为 特别若,称这样的方程组为齐次方程组。称数表为该线性方程组的系数矩阵;称数表为该线性方程组的增广矩阵。事实上,给定了线性方程组,就惟一地确定了它的增广矩阵;反过来,只要给定一个m(n+1)阶矩阵,就能惟一地确定一个以它为增广矩阵的n个未知数,m个方程的线性方程组。例1 写出下面线性方程组的系数矩阵和增广矩阵【答疑编号12020101】例2 写出以下面矩阵为增广矩阵的线性方程组 【答疑编号12020102】2.1.2矩阵的概念一、矩阵的定义定义2.1.1 我们称由mn个数排成的m行n列的数表 为mn阶矩阵,也可记为为矩阵A第i行,第j列的元素。 注意:矩阵和行列式的区别。二、几类特殊的矩阵1.所有元素都为零的矩阵称为零矩阵,记为O。例如都是零矩阵。2.若A的行数m=1,则称 为行矩阵,也称为n维行向量。若A的列数n=1,则称为列矩阵,也称为m维列向量。3.若矩阵A的行数=列数=n,则称矩阵A为n阶方阵,或简称A为n阶阵。如n个未知数,n个方程的线性方程组的系数矩阵。4.称n阶方阵为n阶对角阵。特别若上述对角阵中,称矩阵为数量矩阵,如果其中=1,上述数量阵为,称为n阶单位阵。5.上(下)三角阵称形如的矩阵为上(下)三角矩阵。2.2矩阵的运算 这节介绍(1)矩阵运算的定义,特别要注意,矩阵运算有意义的充分必要条件;(2)矩阵运算的性质,要注意矩阵运算与数的运算性质的异同,重点是矩阵运算性质与数的运算性质的差别。2.2.1矩阵的相等为建立矩阵运算的概念,先说明什么叫两个矩阵相等。定义2.2.1如果矩阵A,的阶数相同,即行数、列数都相同,则称矩阵与B同型;若A与B同型,且对应元素都相等,则称矩阵A与B相等,记为A=B。请注意区别两个矩阵相等和两个行列式相等例如 虽然行列式有但矩阵;。2.2.2矩阵的加减法 定义2.2.2 设A与B都是mn阶矩阵(即A与B同型),则矩阵A与B可以相加(相减),其和(差)定义为mn阶矩阵 例1设求A+B、A-B。【答疑编号12020103】例2则A与B不能相加(减),或说AB无意义。 加法运算的性质设A,B,C都是mn阶矩阵,O是mn阶零矩阵,则1.交换律 A+B=B+A。2.结合律 (A+B)+C=A+(B+C)。3.负矩阵 对于任意的mn阶矩阵定义,显然A+(-A)=O;A-B=A+(-B)。2.2.3数乘运算定义2.2.3 数与矩阵A的乘积记作A或A,定义为 例3 设,求3A。 【答疑编号12020104】解例4 设,求3A-2B。 【答疑编号12020105】例5 已知,求2A-3B。 【答疑编号12020106】数乘运算满足:1.1A=A2.设k,l是数,A是矩阵,则k(lA)=(kl)A3.分配律 k(A+B)=Ka+kB;(k+l)A=kA+lA例6 已知,且A+2X=B,求X。2.2.4矩阵的乘法先介绍矩阵乘法的定义,后面再介绍为什么这样定义乘法。一、定义定义2.2.4 设矩阵,(注意:A的列数=B的行数)。定义A与B的乘积为一个mn阶矩阵,其中(i=1,2,m,j=1,2, n)可见,矩阵A,B可以相乘的充分必要条件是A的列数B的行数,乘积矩阵C=AB的行数=A的行数;其列数=B的列数。例如则A,B可以相乘,其乘积其中例7设矩阵【答疑编号12020201】问BA有意义吗?无意义。因为第一个矩阵的列数不等于第二矩阵的行数,所以BA无意义。例8(1)设矩阵(2)求AB;BA【答疑编号12020202】此例说明 AB,BA虽然都有意义,但两矩阵不同型,当然不相等。例9设矩阵,求AB,BA。【答疑编号12020203】为什么这样定义乘法?考虑线性方程组设,则,于是线性方程组(1)就可以写成矩阵形式AX=b。这表明,应用这种方法定义矩阵乘法,可以把任意线性方程组写成与一元一次方程ax=b完全相同的形式,使整个的讨论变得简单了。二、性质(1)乘法没有交换律,AB不一定等于BA。(2)结合律 (AB)C=A(BC) (3)分配律 (A+B)C=AC+BC;A(B+C)=AB+AC (4)数乘与乘法的结合律k(AB)=(kA)B=A(kB)(5)单位矩阵的作用。另一部分的证明请同学们自己作。但对于某些特殊的矩阵(方阵)满足AB=BA,我们称它们是乘法可交换的,例如n阶方阵A与n阶单位阵就可交换。例10 设矩阵,求出所有与A乘积可交换的矩阵。【答疑编号12020204】2.2.5方阵的幂设A是一个矩阵,何时有意义?当且只当A为n阶方阵时,有意义。这时,对k2定义称为A的k次幂。例11 数学归纳法证明【答疑编号12020301】(2)【答疑编号12020302】对于数,幂的运算有下列性质:(1)同底幂相乘,指数相加。即;(2);(3)对于方阵的幂有下列性质:(1)。对于数,为什么所以对于n阶方阵不一定等于。根据矩阵乘法和方阵幂的性质,数的乘法公式有下面的变化:一般不等于。一般不等于。这些变化的原因就在于矩阵乘法没有交换律。但对于某些特殊的矩阵满足AB=BA,例如n阶方阵A与n阶单位阵就可交换,所以请思考例12 设求。【答疑编号12020303】例13 设,求。【答疑编号12020304】例14 设。【答疑编号12020305】小结 矩阵乘法和数的乘法性质的区别:(1)矩阵乘法没有交换律,由此引出乘法公式:如,不一定等于等公式的变化;(2)对于矩阵:两个非零矩阵的乘积可能为零矩阵;(3)对于方阵,可能可能,(4)不一定等于。2.2.6矩阵的转置一、定义定义2.2.5设。将其行列互换,所得的矩阵记为称它为A的转置,即显然,mn阶矩阵A的转置是nm阶。二、性质1.;2.;3.;现看下面的例例15 设,求;问哪个有意义,若有意义,求它的乘积矩阵。【答疑编号12020306】解没有
更多 “自学考试专题:高等教育自学考试网上辅导线性代数(经管类)第2章” 相关考题
- 财税(2016)36号、(2016)18号公告中的“预收款方式销售”是指全额预收吗?
- 多选题党的十八届五中全会强调,坚定走的文明发展道路的基本特征是()。A生产发展B生活富裕C生命保障D生态良好
- 中国人寿提出了以下问题,保险代理人中有两名是残疾人,在营改增之前,残疾人月佣金收入超过3万元起征点免营业税,当时地税局是将两名残疾人办成了个体工商户身份,并为其做了营业税免税备案。营改增后,根据36号文附件3,残疾人员本人为社会提供的服务免征增值税,那么这两名残疾人如何在国税接受免税管理,是否也要参照地税的方法?
- 单选题()是发展的第一动力。A 改革B 创新C 发展
- 购买农产品的买价,是指纳税人购进农产品在农产品收购发票或者销售发票上注明的价款和按照规定缴纳的()A、契税B、农业税C、烟叶税D、烟草税
- 单选题反映门(急)诊工作效率的指标是()。A 门(急)诊人次和抢救人次B 平均开放病床数C 急诊抢救成功率D 七日确诊率E 病床使用率
- 单选题电子病案文本编辑中自然语言处理是为了()。A 建立结构化系统模型B 将数字化医学信息整合到电子病案中C 从自由文本上提取代码化的医学数据D 协助临床诊断、治疗E 定义专业词汇
- 单选题病案管理现代化的意义包括()。A 适应医学科学的发展B 对医院进行科学化管理,提高医疗技术C 引发病案管理模式新的变革D 病案信息能高度共享E 以上均是
- 司马迁的《史记》记载了商王的世系,但长期以来并不能确定该记载是否真实。19世纪末20世纪初殷墟甲骨文的发现,证实《史记》的记载基本上是正确的。这说明()A、考古资料比文献材料更真实B、历史记载不存在纯粹客观性C、历史记载必须经过考古发现证实D、考古发现是历史研究的重要依据
- 为企业培训提供会议室(不组织培训)、住宿、餐饮等所有服务,按参加培训的人员的人头收取每人一定额度的固定费用,是否可以全部开培训费?应该怎样开具发票?如果全开培训费,对方取得后,餐饮部分是否可以全部抵扣?
- 山东省菏泽市牡丹区王浩屯中学2022-2023学年中考适应性考试英语试题(含解析)-
- 内蒙古阿荣旗第一中学2022-2023学年高三3月份第一次模拟考试英语试卷含解析-
- 内蒙古自治区兴安盟乌兰浩特市卫东中学2022-2023学年中考英语适应性模拟试题(含解析)-
- 山东省济南长清区六校联考2022-2023学年十校联考最后英语试题(含解析)-
- 内蒙古阿拉善盟右旗重点达标名校2022-2023学年中考四模英语试题(含解析)-
- 七年级英语下册Unit7It'sraining第5课时学案无答案新版人教新目标版-
- 七年级英语下册Unit4Don'teatinclass第5课时学案无答案新版人教新目标版-
- 山东省济宁邹城县联考2022-2023学年中考英语全真模拟试题(含解析)-
- 山东省东明县2022-2023学年中考英语全真模拟试题(含解析)-
- 2020年春七年级英语下册Unit5OurSchoolLifeTopic3MyschoollifeisveryinterestingSectionD作业无答案新版仁爱版-