网友您好, 请在下方输入框内输入要搜索的题目:
△ABC中,设∠A=a,则∠B、∠C的平分线的交角是______,∠B、∠C的外角平分线的交角是______,∠B的平分线与∠C的外角平分线相交成的锐角度数是______.
90°+
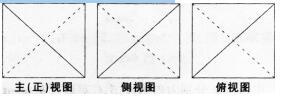
B.√3
C.2√3
D.4√3


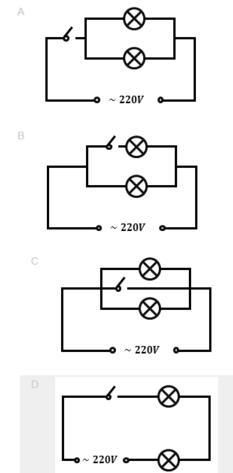
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
A.45.4 cm B.45.1 cm C.44.8 cm D.44.5 cm
山东省泰安市2022年中考数学真题一、单选题1|5| 的倒数是() A15B15C5D52计算(a3)2a3的结果是() Aa8Ba9Ca10Da113某种零件模型如图所示,该几何体(空心圆柱)的俯视图是() ABCD4如图,ABC的外角ACD的平分线CP与内角ABC的平分线BP交于点P,若BPC40,则CAP() A40B45C50D605某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是()A15.5,15.5B15.5,15C15,15.5D15,156某工程需要在规定时间内完成,如果甲工程队单独做,恰好如期完成; 如果乙工程队单独做,则多用3天,现在甲、乙两队合做2天,剩下的由乙队单独做,恰好如期完成,求规定时间.如果设规定日期为x天,下面所列方程中错误的是()A2x+xx+3=1B2x=3x+3C(1x+1x+3)2+x2x+3=1D1x+xx+3=17如图,函数 y=ax22x+1 和 y=axa ( a 是常数,且 a0 )在同一平面直角坐标系的图象可能是()ABCD8已知方程3aa4a=14a,且关于x的不等式axb只有4个整数解,那么b的取值范围是()A2b3B3b4C2b3D3b49如图,点I为的ABC内心,连接AI并延长交ABC的外接圆于点D,点E为弦AC的中点,连接CD,EI,IC,当AI=2CD,IC=6,ID=5时,IE的长为()A5B4.5C4D3.510一元二次方程14x2+2x+12=53x+15根的情况是()A有一个正根,一个负根B有两个正根,且有一根大于9小于12C有两个正根,且都小于12D有两个正根,且有一根大于1211如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1, ABC 经过平移后得到 A1B1C1 ,若 AC 上一点 P(1.2,1.4) 平移后对应点为 P1 ,点 P1 绕原点顺时针旋转 180 ,对应点为 P2 ,则点 P2 的坐标为()A(2.8,3.6)B(2.8,3.6)C(3.8,2.6)D(3.8,2.6)12如图,AOB=30,点M、N分别在边OA、OB上,且OM=3,ON=5,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是()A34B35C342D352二、填空题13地球的体积约为1012立方千米,太阳的体积约为1.41018立方千米,地球的体积约是太阳体积的倍数是 (用科学记数法表示,保留2位有效数字) 14如图, ABC 中,BAC=90,AB=3,AC=4,点 D 是 BC 的中点,将 ABD 沿 AD 翻折得到 AED,连 CE,则线段 CE 的长等于 15如图,将半径为2,圆心角为120的扇形OAB绕点A逆时针旋转60,点O,B的对应点分别为O,B,连接BB,则图中阴影部分的面积是 16观察下列图形规律,当图形中的“”的个数和“”个数差为2022时,n的值为 17如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30,已知斜坡的斜面坡度i=1:3,且点A,B,C,D,在同一平面内,小明同学测得古塔AB的高度是 18如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB= 5 .下列结论:APDAEB;点B到直线AE的距离为 2 ;EBED;SAPD+SAPB=1+ 6 ;S正方形ABCD=4+ 6 .其中正确结论的序号是 . 三、解答题19 (1)若单项式xmny14与单项式12x3y3m8n是一多项式中的同类项,求m、n的值;(2)先化简,再求值:(xx+1+1x1)1x21,其中x=2120如图,反比例函数ymx的图象与一次函数ykxb的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1)(1)求反比例函数与一次函数的表达式;(2)点E为y轴上一个动点,若SAEB5,求点E的坐标21为庆祝中国共产党建党100周年,某校加强了学生对党史知识的学习,并组织学生参加党史知识测试(满分100分)为了解学生对党史知识的掌握程度,从七、八年级中各随机抽取10名学生的测试成绩,进行统计、分析,过程如下:收集数据:七年级:86 88 95 90 100 95 95 99 93 100八年级:100 98 98 89 87 98 95 90 90 89整理数据:成绩x(分)年级85x9090x9595x100七年级343八年级5ab分析数据:统计量年级平均数中位数众数七年级94.195d八年级93.4c98应用数据:(1)填空:a= ,b= ,c= ,d= ;(2)若八年级共有200人参与答卷,请估计八年级测试成绩大于95分的人数;(3)从测试成绩优秀的学生中选出5名语言表达能力较强的学生,其中八年级3名,七年级2名.现从这5名学生中随机抽取2名到当地社区担任党史宣讲员请用画树状图或列表的方法,求恰好抽到同年级学生的概率22某电子商品经销店欲购进A、B两种平板电脑,若用9000元购进A种平板电脑12台,B种平板电脑3台;也可以用9000元购进A种平板电脑6台,B种平板电脑6台(1)求A、B两种平板电脑的进价分别为多少元?(2)考虑到平板电脑需求不断增加,该商城准备投入3万元再购进一批两种规格的平板电脑,已知A型平板电脑售价为700元/台,B型平板电脑售价为1300元/台根据销售经验,A型平板电脑不少于B型平板电脑的2倍,但不超过B型平板电脑的2.8倍假设所进平板电脑全部售完,为使利润最大,该商城应如何进货?23正方形ABCD中,P为AB边上任一点,AEDP于E,点F在DP的延长线上,且DE=EF,连接AF、BF,BAF的平分线交DF于G,连接GC(1)求证:AEG是等腰直角三角形;(2)求证:AG+CG=2DG;(3)若AB=2,P为AB的中点,求BF的长24如图,抛物线y=mx2+3mx2m+1的图象经过点C,交x轴于点A(x1,0),B(x2,0)(点A在点B左侧),且x2x1=5连接BC,D是AC上方的抛物线一点(1)求抛物线的解析式;(2)连接BC,CD,SDCE:SBCE是否存在最大值?若存在,请求出其最大值及此时点D的坐标;若不存在,请说明理由(3)第二象限内抛物线上是否存在一点D,DF垂直AC于点F,使得DCF中有一个锐角等于与BAC的两倍?若存在,求点D得横坐标,若不存在,请说明理由25如图,四边形ABCD中,AB=AD=CD,以AB为直径的O经过点C,连接AC,OD交于点E(1)证明:ODBC;(2)若tanABC=2,证明:DA与O相切;(3)在(2)条件下,连接BD交于O于点F,连接EF,若BC=1,求EF的长答案解析部分1【答案】A2【答案】B3【答案】C4【答案】C5【答案】D6【答案】D7【答案】B8【答案】D9【答案】C10【答案】D11【答案】A12【答案】A13【答案】7.110-714【答案】7515【答案】232316【答案】不存在17【答案】(20+103)m18【答案】19【答案】(1)解:由题意可得mn=33m8n=14,3,可得:5n=5,解得:n=1,把n=1代入,可得:m(1)=3,解得:m=2,m的值为2,n的值为-1;(2)解:原式=x(x1)+(x+1)(x+1)(x1)(x+1)(x1)=x2x+x+1(x+1)(x1)(x+1)(x1)=x2+1,当x=21时,原式=(21)2+1=222+1+1=42220【答案】(1)解:把点A(2,6)代入ymx,得m12,则y12x把点B(n,1)代入y12x,得n12,则点B的坐标为(12,1)由直线ykxb过点A(2,6),点B(12,1)得2k+b=612k+b=1,解得k=12b=7,则所求一次函数的表达式为y12x7;(2)解:如图,直线AB与y轴的交点为P,设点E的坐标为(0,m),连接AE,BE,则点P的坐标为(0,7)PE|m7|SAEBSBEPSAEP5,12|m7|(122)5|m7|1m16,m28点E的坐标为(0,6)或(0,8)21【答案】(1)1;4;92.5;95(2)解:200410=80,估计八年级测试成绩大于95分的人数为80人(3)解:画树状图为:共有20种等可能的结果,其中两同学为同年级的结果数为8,所以抽到同年级学生的概率=820=2522【答案】(1)解:设A、B两种平板电脑的进价分别为x元、y元由题意得,12x+3y=90006x+6y=9000,解得x=500y=1000,答:A、B两种平板电脑的进价分别为500元、1000元;(2)解:设商店准备购进B种平板电脑a台,则购进A种平板电脑300001000a500台,由题意,得 2a300001000a500300001000a5002.8a,解得12.5a15,a为整数,a=13或14或15设总利润为w,则:w=(700-500)300001000a500+(1300-1000)a=-100a+12000,-1000,w随a的增大而减小,为使利润最大,该商城应购进B种平板电脑13台,A种平板电脑3000010001350034台答:购进B种平板电脑13台,A种平板电脑34台23【答案】(1)证明:DE=EF,AEDP,AF=AD,AFD=ADF,ADF+DAE=PAE+DAE=90,AFD=PAE,AG平分BAF,FAG=GAPAFD+FAE=90,AFD+PAE+FAP=902GAP+2PAE=90,即GAE=45,AGE为等腰直角三角形;(2)证明:作CHDP,交DP于H点,DHC=90AEDP,AED=90,AED=DHCADE+CDH=90,CDH+DCH=90
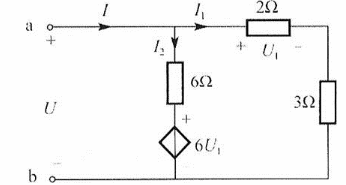
B.30Ω
C.-15Ω
D.15Ω
A.45.4 cm B.45.1 cm C.44.8 cm D.44.5 cm
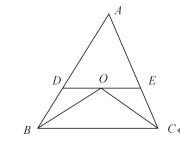
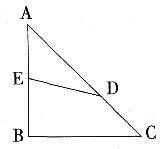
如图所示,ΔABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与ΔAED的面积之比为3:2。问AE的长度是多少?()
A.6.9
B.7.1
C.7.2
D.7.4
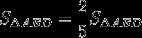 ,即
,即 ×AE×
×AE× ×12=
×12= ×
× ×12×12,得AE=7.2。
×12×12,得AE=7.2。
B. 20°
C. 25°
D. 30°


B. 20°
C. 25°
D. 30°

更多 “山东省泰安市2022年中考数学真题及答案” 相关考题
- 多选题生产经营单位的从业人员有权了解其作业场所和工作岗位存在的()。A危险因素B风险C特点D防范措施E事故应急措施
- 造成曲轴承载后的弯曲变形的原因有()。A、发动机在爆震和超负荷条件下工作B、个别汽缸不工作或工作不均衡C、各道主轴承松紧度不一致D、主轴承座孔同轴度偏差增大
- 单选题下列关于收集资料的叙述,错误的是【 】A 资料可来源于现有资料和新收集的资料B 某些历史性研究可从现有的资料,例如期刊、日记、信件、报纸、会议记录、病史、报告等处收集C 对现有资料可直接应用,不用评估和分析其价值、准确性D 利用现有资料的方法具有省时、省力、经济的特点,但应根据研究目的而定
- 判断题建筑工程设计应当符合按照国家规定制定的建筑安全规程和技术规范,保证工程的安全性能。A 对B 错
- 简述制动系统常见故障?
- 判断题安全生产费用是指企业按照规定标准提取,在成本中列支,专门用于完善和改进企业安全生产条件的资金。A 对B 错
- 问答题简述右心衰竭时发生水肿的机制。
- 判断题阳台栏板应随层安装,不能随层安装的,必须在阳台处派专人看护。A 对B 错
- 单选题塑料安全帽的使用期限不应超过()。A 2年半B 3年C 3年半D 5年
- 在修理空调压缩机离合器时,甲说:要在转盘和衔铁之间涂一层轻质润滑油;乙说:要用塞尺检查转子与衔铁之间的间隙。试问谁正确?()A、甲正确;B、乙正确;C、两人均正确;D、两人均不正确