网友您好， 请在下方输入框内输入要搜索的题目：

2019年全国高考理科数学试题分类汇编16：不等式选讲

已知集合A={x|x≤1},B={x|≥a},且A∪B=R，

则实数a的取值范围是__________________.


正确答案：
 2.ɑ≤1 

求不等式5x－1>3(x＋1)与x ／2 －1<7－3 x／2的解集的公共部分。

求不等式5x-1＞3（x+1）与x/2-1<7-3 x/2的解集的公共部分。


5x-1>3x+3                   x-2<14-3x

x>2                        x<4

              2<x<4


已知关于x的方程3x+a=x-7的根是正数，求实数a的取值范围。


解原方程得x=-(7+a)/2>0

得a<-7


将下列不等式化成“x>a"或“x27;(3)x

将下列不等式化成“x＞a"或“x＜a"的形式：

（1）x+3＜-1；    （2）3x＞27；

（3）x/3＞5；     （4）5x＜4x-6。


(1)x<-4          (2)x>9

(3)x<-15           (4)x<-6


若对于任意实数x,都有t2+5t ≤|2x-4|-|x+2|恒成立,则t的取值范围是( ).

(A)[1,4].

(B)[-4,-1].

(C)(-∞,1]∪[4,+∞).

(D)(-∞,-4]∪[-1,+∞).


参考答案B

摘要:2019年全国高考理科数学试题分类汇编16：不等式选讲一、填空题1．（2019年普通高等学校招生统一考试重庆数学（理）试题（含答案））若关于实数x的不等式x5x3a无解,则实数a的取值范围是_________【答案】�,82．（2019年高考陕西卷（理））(不等式选做题)已知a,b,m,n均为正数,且a+b=1,mn=2,则(am+bn)(bm+an)的最小值为_______.【答案】23．（2019年高考江西卷（理））(不等式选做题)在实数范围内,不等式x21�1的解集为_________【答案】0,44．（2019年高考湖北卷（理））设x,y,z�R,且满足:x2y2z21,x2y3z14,则xyz_______.【答案】3147二、解答题5．（2019年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD版含答案））选修4—5;不等式选讲设a,b,c均为正数,且abc1,证明:13(Ⅰ)abbcca�;(Ⅱ)【答案】a2b2c2�1.bca 6．（2019年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））选修4-5:不等式选讲已知函数fxxa,其中a1.(I)当a=2时,求不等式fx�4x4的解集;(II)已知关于x的不等式f2xa2fx�2的解集为x|1�x�2,求a的值.【答案】7．（2019年普通高等学校招生统一考试福建数学（理）试题（纯WORD版））不等式选讲:设不等式31x2a(a�N*)的解集为A,且�A,�A.22(1)求a的

若分式1/（x-5）有意义，则实数x的取值范围是__________。


正确答案：

分析：由于分式的分母不能为0，x－5在分母上，因此x－5≠0，解得x≠5。
答案：
涉及知识点：分式的意义
点评：初中阶段涉及有意义的地方有三处，一是分式的分母不能为0，二是二次根式的被开方数必须是非负数，三是零指数的底数不能为零。
推荐指数：★★★

关于x的方程2cos2x-sinx+a0在区间[0，7π/6]上恰好有两个不等实根，则实数a的取值范围是_____。


答案：
解析：

已知关于x的方程x2-2(k-1)x+k2有两个实数根x1，x2。
(1)求k的取值范围；
(2)若|x1-x2|=x1x2-1，求k的值。


答案：
解析：

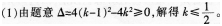
(2)由方程有x1+x2=2(k-1)，x1x2=k2。若x1-x2=x1x2-1，贝4(x1+x2)2-4x1x2=x1x2-1)2，即4(k-1)2-4k2=(k2-1)2，即(k2-2k+3)(k2+2k-1)=0，解得

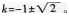
已知集合A={x|x2-3x-4>0}，集合B={x|m+1≤x≤4m}，若B?A，则实数m的取值范围为()。

A.(-∞，3)
B.(-(1/4)，3)
C.(-∞，-(1/4))∪(3，+∞)
D.(-∞，1/3)∪(3，+∞)

答案：D
解析：

已知二次函数f(x)的二次项系数为实数a，且其图像与直线2x+y=0交点横坐标为1和3．
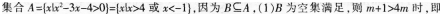
(1)若方程f(x)+6a=0有两个相等的实数根，求f(x)的解析式；
(2)若f(x)的最大值为正数，求实数n的取值范围．


答案：
解析：
解：根据题意f(x)与2x+y=0的交点为(1，-2)、(3，-6)，设f(x)=ax2+bx+c，将上述两个交点代入，有a+b+c=-2，9a+36+c=-6，整理可得b=-2-4a，c=3a.

更多 “2019年全国高考理科数学试题分类汇编16：不等式选讲” 相关考题
考题 不等式∣x+3∣-∣x-1∣≤a2-3a对任意实数x恒成立,则实数a的取值范围为A.（-∞,-1]U[4,+∞） B.（一∞,一2]U[5,+∞） C.[1,2] D.（一∞,1]U[2,+∞） E.以上选项均不正确答案：A解析：∣x+3∣-∣x-1∣≤4，a2-3a≥4,解得a≤-1或a≥4
查看答案
考题 单选题若关于x的方程x2＋2x＋a＝0不存在实数根，则a的取值范围是（　　）．A a＜1B a＞1C a≤1D a≥1正确答案： B 解析： 由4－4a＜0，故a＞1．
查看答案
考题 填空题能够使不等式(|x|－x)(1＋x)＜0成立的x的取值范围是____．正确答案： x-1 解析： 当x≥0时，|x|－x＝x－x＝0，于是(|x|－x)(1＋x)＝0，不满足原式，故舍去x≥0．当x＜0时，|x|－x＝－2x＞0，x应当要使(|x|－x)(1＋x)＜0，满足1＋x＜0，即x＜－1，所以x的取值范围是x＜－1．
查看答案
考题 填空题若不等式x2－ax－b＜0的解集是{x|2＜x＜3}，则a＋b＝____．正确答案： -1 解析： 由题可知，2和3应为方程x2－ax－b＝0的两个根．根据根与系数的关系，2＋3＝a，2×3＝－b，即a＝5，b＝－6．a＋b＝－1．
查看答案
考题 满足不等式（x+4）（x+6）+3>0的所有实数的集合是A.[4,+∞） B.（4,+∞） C.（-∞,-2] D.（-∞,-1] E.（-∞,+∞）答案：E解析：
查看答案
考题 填空题若不等式x2－ax－b＜0的解集是{x|2＜x＜3}，则a＋b＝____．正确答案： -1 解析： 由题可知，2和3应为方程x2－ax－b＝0的两个根．根据根与系数的关系，2＋3＝a，2×3＝－b，即a＝5，b＝－6．a＋b＝－1．
查看答案
考题 填空题能够使不等式(|x|－x)(1＋x)＜0成立的x的取值范围是____．正确答案： x-1 解析： 当x≥0时，|x|－x＝x－x＝0，于是(|x|－x)(1＋x)＝0，不满足原式，故舍去x≥0．当x＜0时，|x|－x＝－2x＞0，x应当要使(|x|－x)(1＋x)＜0，满足1＋x＜0，即x＜－1，所以x的取值范围是x＜－1．
查看答案
考题 填空题若不等式x2－ax－b＜0的解集是{x|2＜x＜3}，则a＋b＝____．正确答案： -1 解析： 由题可知，2和3应为方程x2－ax－b＝0的两个根．根据根与系数的关系，2＋3＝a，2×3＝－b，即a＝5，b＝－6．a＋b＝－1．
查看答案
考题 单选题关于x的不等式x－b＞0恰有两个负整数解，则b的取值范围是（　　）．A －3＜b＜－2B －3＜b≤－2C －3≤b≤－2D －3≤b＜－2正确答案： A 解析： 因为x－b＞0，所以x＞b；x有两个负整数解，故这两个负整数一定是－1和－2，所以－3≤x＜－2．
查看答案
考题 单选题在画图软件中，输入“plot[sin[x]，{x，-pi，pi}]”，则图像为：（）。A sinx，x取值[-π，π]B sinx，x取值为全体实数C cosx，x取值[-π，π]D cosx，x取值为全体实数正确答案： D 解析： 暂无解析
查看答案
热门标签
最新考题
最新试卷
热门试卷