网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
在《普通高中数学课程标准(实验)》q-关于“二元一次不等式组与简单线性规划问题”的内容及要求如下:
①从实际情境中抽象出二元一次不等式组。
②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组。
③从实际情境中抽象出一些简单的二元线性规划问题.并能加以解决。
结合必修5“简单的线性规划问题”这一节的内容,完成下列设计。
(1)确定本节课的教学目标:
(2)确定本节课的教学重点和难点:
(3)给出本节课的教学过程。
①从实际情境中抽象出二元一次不等式组。
②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组。
③从实际情境中抽象出一些简单的二元线性规划问题.并能加以解决。
结合必修5“简单的线性规划问题”这一节的内容,完成下列设计。
(1)确定本节课的教学目标:
(2)确定本节课的教学重点和难点:
(3)给出本节课的教学过程。
参考答案
参考解析
解析:(1)教学目标:
知识与技能
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;
2.运用线性规划问题的图解法,并能应用它解决一些简单的实际问题。
过程与方法
1.培养观察、联想以及作图的能力,渗透集合、化归、数形结合的数学思想,提高“建模”和解决实际问题的能力:
2.结合教学内容。提高学习数学的兴趣和“用数学”的意识,勇于创新。
情感态度与价值观
1.通过本节教学着重培养掌握“数形结合”的数学思想,尽管侧重于用“数”研究“形”,但同时也用“形”去研究“数”,培养观察、联想、猜测、归纳等数学能力;
2.结合教学内容,培养学习数学的兴趣和“用数学”的意识,勇于创新。
(2)教学重点:二元一次不等式(组)表示平面的区域。
教学难点:把实际问题转化为线性规划问题,并给出解答。解决难点的关键是根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解。为突出重点,本节教学应引导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何化。
(3)教学过程
导入新课师前面我们学习了二元一次不等式Ax+By+C>O在平面直角坐标系中的平面区域的确定方法。请同学们回
忆一下。
(生回答)
推进新课
[合作探究]
(1)教学目标:
知识与技能
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;
2.运用线性规划问题的图解法,并能应用它解决一些简单的实际问题。
过程与方法
1.培养观察、联想以及作图的能力,渗透集合、化归、数形结合的数学思想,提高“建模”和解决实际问题的能力:
2.结合教学内容。提高学习数学的兴趣和“用数学”的意识,勇于创新。
情感态度与价值观
1.通过本节教学着重培养掌握“数形结合”的数学思想,尽管侧重于用“数”研究“形”,但同时也用“形”去研究“数”,培养观察、联想、猜测、归纳等数学能力;
2.结合教学内容,培养学习数学的兴趣和“用数学”的意识,勇于创新。
(2)教学重点:二元一次不等式(组)表示平面的区域。
教学难点:把实际问题转化为线性规划问题,并给出解答。解决难点的关键是根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解。为突出重点,本节教学应引导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何化。
(3)教学过程
导入新课师前面我们学习了二元一次不等式Ax+By+C>O在平面直角坐标系中的平面区域的确定方法。请同学们回
忆一下。
(生回答)
推进新课
[合作探究]




[知识拓展]




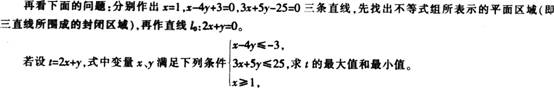
[合作研究]



知识与技能
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;
2.运用线性规划问题的图解法,并能应用它解决一些简单的实际问题。
过程与方法
1.培养观察、联想以及作图的能力,渗透集合、化归、数形结合的数学思想,提高“建模”和解决实际问题的能力:
2.结合教学内容。提高学习数学的兴趣和“用数学”的意识,勇于创新。
情感态度与价值观
1.通过本节教学着重培养掌握“数形结合”的数学思想,尽管侧重于用“数”研究“形”,但同时也用“形”去研究“数”,培养观察、联想、猜测、归纳等数学能力;
2.结合教学内容,培养学习数学的兴趣和“用数学”的意识,勇于创新。
(2)教学重点:二元一次不等式(组)表示平面的区域。
教学难点:把实际问题转化为线性规划问题,并给出解答。解决难点的关键是根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解。为突出重点,本节教学应引导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何化。
(3)教学过程
导入新课师前面我们学习了二元一次不等式Ax+By+C>O在平面直角坐标系中的平面区域的确定方法。请同学们回
忆一下。
(生回答)
推进新课
[合作探究]
(1)教学目标:
知识与技能
1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;
2.运用线性规划问题的图解法,并能应用它解决一些简单的实际问题。
过程与方法
1.培养观察、联想以及作图的能力,渗透集合、化归、数形结合的数学思想,提高“建模”和解决实际问题的能力:
2.结合教学内容。提高学习数学的兴趣和“用数学”的意识,勇于创新。
情感态度与价值观
1.通过本节教学着重培养掌握“数形结合”的数学思想,尽管侧重于用“数”研究“形”,但同时也用“形”去研究“数”,培养观察、联想、猜测、归纳等数学能力;
2.结合教学内容,培养学习数学的兴趣和“用数学”的意识,勇于创新。
(2)教学重点:二元一次不等式(组)表示平面的区域。
教学难点:把实际问题转化为线性规划问题,并给出解答。解决难点的关键是根据实际问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解。为突出重点,本节教学应引导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何化。
(3)教学过程
导入新课师前面我们学习了二元一次不等式Ax+By+C>O在平面直角坐标系中的平面区域的确定方法。请同学们回
忆一下。
(生回答)
推进新课
[合作探究]




[知识拓展]




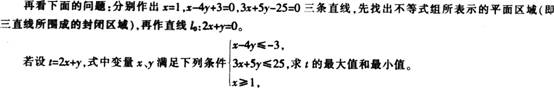
[合作研究]



更多 “在《普通高中数学课程标准(实验)》q-关于“二元一次不等式组与简单线性规划问题”的内容及要求如下: ①从实际情境中抽象出二元一次不等式组。 ②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组。 ③从实际情境中抽象出一些简单的二元线性规划问题.并能加以解决。 结合必修5“简单的线性规划问题”这一节的内容,完成下列设计。 (1)确定本节课的教学目标: (2)确定本节课的教学重点和难点: (3)给出本节课的教学过程。” 相关考题
考题
高中数学《均值不等式》
一、考题回顾
题目来源:5月19日 上午 江西省南昌市 面试考题
试讲题目
1.题目:均值不等式
2.内容:
3.基本要求:
(1)引导学生理解、证明均值不等式;
(2)教学中注意师生间的交流互动,有适当的提问环节。
(3)要求配合教学内容有适当的板书设计。
(4)请在10分钟内完成试讲内容。
答辩题目
1.利用均值不等式如何求最值问题?
2.本节课的重难点是什么?
考题
关于“血糖平衡的调节”,《普通高中生物课程标准(实验)》的内容标准是:描述血糖调节。某教材关于该内容的具体呈现如下:
(1)设计血糖调节的图解式模型。
(2)设计“建立血糖调节的模型”的教学过程。
考题
《普通高中数学课程标准(实验)》将“( )、数学建模、数学文化”作为贯穿整个高中数学课程的重要学习活动,渗透或安排在每个模块或专题中,正是与创新能力培养的一个呼应,强调如何引导学生去发现问题、提出问题。A.数学探究
B.数学应用
C.数学思想
D.数学概念
考题
《普通高中数学课程标准(实验)》设置了四个选修系列,其中选修系列2是为希望在理工、经济等方面发展的学生而设置的,下列内容不属于选修系列2的是( )。
A、导数及其应用
B、圆锥曲线与方程
C、统计案例
D、框图
考题
《普通高中数学课程标准实验标准(实验)》设置了四个选修系列,其中选修系列2是希望在理工、经济类方面发展的学生而设置的,下列内容不属于选修系列2的是( )A.矩阵变换
B.推理能力
C. 导数及应用
D.常用逻辑用语
考题
《普通高中数学课程标准(实验)》设置了四个选修系列,其中选修系列l是为希望在人文社会科学等方面发展学生而设置的,下列内容不属于选修系列1的是( )。
A、矩阵变换
B、推理证明
C、导数及应用
D、常用逻辑用语
考题
“数列”是高中数学必修5的内容。《普通高中数学课程标准(实验)》要求学生能“通过对日常生活中大量实际问题的分析,建立等差数列和等比数列这两种数列模型;在具体的问题情境中.发现数列的等差关系或等比关系,并能用有关知识解决相应的问题。”
(1)请设计一道能用等比数列知识解决的实际问题并求解;(20分)
(要求:给出问题情境;抽象出数量关系;建立数学模型;写出解答过程、讨论和反思。)
(2)根据上面的问题情境设计一道开放题或探索题。(10分)
考题
《普通高中数学课程标准(实验)》将“( )、数学建模、数学文化”作为贯穿整个高中数学课程的重要学习活动,渗透或安排在每个模块或专题中,正是与创新能力培养的一个呼应,强调如何引导学生去发现问题、提出问题。
A、数学探究
B、数学应用
C、数学思想
D、数学概念
考题
下列关于线性规划叙述正确的是()。A、线性规划问题,若有最优解,则必是一个基变量组的可行基解B、线性规划问题一定有可行基解C、线性规划问题的最优解只能在最低点上达到D、单纯型法求解线性规划问题时,每换基迭代一次必使目标函数值下降一次
考题
单选题下列关于线性规划叙述正确的是()。A
线性规划问题,若有最优解,则必是一个基变量组的可行基解B
线性规划问题一定有可行基解C
线性规划问题的最优解只能在最低点上达到D
单纯型法求解线性规划问题时,每换基迭代一次必使目标函数值下降一次
考题
单选题下列哪种学习方式不是《普通高中数学课程标准(实验)》所提倡的?()A
合作学习B
探究学习C
机械学习D
自主学习
热门标签
最新试卷