网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
高中数学《均值不等式》
一、考题回顾
题目来源:5月19日 上午 江西省南昌市 面试考题
试讲题目
1.题目:均值不等式
2.内容:

3.基本要求:
(1)引导学生理解、证明均值不等式;
(2)教学中注意师生间的交流互动,有适当的提问环节。
(3)要求配合教学内容有适当的板书设计。
(4)请在10分钟内完成试讲内容。
答辩题目
1.利用均值不等式如何求最值问题?
2.本节课的重难点是什么?
一、考题回顾
题目来源:5月19日 上午 江西省南昌市 面试考题
试讲题目
1.题目:均值不等式
2.内容:

3.基本要求:
(1)引导学生理解、证明均值不等式;
(2)教学中注意师生间的交流互动,有适当的提问环节。
(3)要求配合教学内容有适当的板书设计。
(4)请在10分钟内完成试讲内容。
答辩题目
1.利用均值不等式如何求最值问题?
2.本节课的重难点是什么?
参考答案
参考解析
解析:二、考题解析
【教学过程】
提出问题:你能在这个图中找出一些相等关系或不等关系吗?
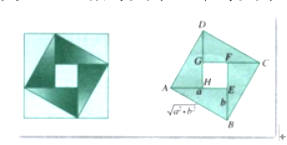
引出本节课题:《均值不等式》。
(二)讲解新知
学生活动:利用导入几何图推导不等式。


2.本节课的重难点是什么?
【参考答案】
并且我认为一节好的数学课,从教学内容上说一定要突出重点、突破难点。根据授课内容我确定本节课的教学重点是:基本不等式的形式以及推导过程。而作为高中内容,命题的严谨性是必要的,所以本节课的教学难点是:基本不等式的推导以及证明过程。
【教学过程】
提出问题:你能在这个图中找出一些相等关系或不等关系吗?

引出本节课题:《均值不等式》。
(二)讲解新知
学生活动:利用导入几何图推导不等式。


2.本节课的重难点是什么?
【参考答案】
并且我认为一节好的数学课,从教学内容上说一定要突出重点、突破难点。根据授课内容我确定本节课的教学重点是:基本不等式的形式以及推导过程。而作为高中内容,命题的严谨性是必要的,所以本节课的教学难点是:基本不等式的推导以及证明过程。
更多 “高中数学《均值不等式》 一、考题回顾 题目来源:5月19日 上午 江西省南昌市 面试考题 试讲题目 1.题目:均值不等式 2.内容: 3.基本要求: (1)引导学生理解、证明均值不等式; (2)教学中注意师生间的交流互动,有适当的提问环节。 (3)要求配合教学内容有适当的板书设计。 (4)请在10分钟内完成试讲内容。 答辩题目 1.利用均值不等式如何求最值问题? 2.本节课的重难点是什么?” 相关考题
考题
小明、小华、小刚三人在一起讨论一个一元一次不等式组。小明:它的所有解为非负数;小华:其中一个不等式的解集为x≤8;小刚:其中一个不等式在求解的过程中需要改变不等号的方向。请你试着写出符合上述条件的不等式组,并解这个不等式组。
考题
初中数学《不等式的性质》
一、考题回顾
二、考题解析
【教学过程】
(一)引入新课
复习导入,先复习等式的性质,并提问学生:不等式是否也有类似的性质,进而引出这节课的课题——不等式的性质。
(二)探索新知
PPT展示4个式子,分别为15___12,15+3___12+3,15-3___12-3,15×3___12×3。
学生活动:填上符号,并观察前3个式子,猜想对于一般的不等式是否也有这样的性质。
教师提示学生类比等式性质1,总结不等式的这条性质,并及时纠正问题(可设置纠错环节),得到性质1:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变;
接着由学生观察最后一个式子,小组活动对比等式两边都城乘(或除)同一个数的性质,说一说不等式的性质。
学生活动,思考将题中的3换成-3,不等式的性质是否成立?并猜想不等式的性质应该怎么表述。
预设学生能够回答不等式的性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变。性质3:不等式两边都乘(或除以)同一个负数,不等号的方向改变。
由学生自由地列举一些符合不等式性质的式子,并与同桌分享。
(三)课堂练习
教师提问学生:不等式的性质与等式的性质有何区别?
学生思考后给出答案,由教师总结:乘除法时,要认清乘(除)的是正数还是负数,负数不等号方向要改变。
尝试利用不等式的性质解-4x>3
并说一说用的哪一条性质。
(四)小结作业
提问:今天有什么收获?
引导学生回顾:不等式的3条性质,等式性质与不等式性质的异同点。
课后作业:
思考不等式的性质除了这3条还有没有其他的性质。
【板书设计】
? ? ?不等式的性质
? ? ?性质1:
? ? ?性质2:
? ? ?性质3:
? ? ?异同点:
1.本节课的教学目标是什么?
2.本节课是用什么方法进行导入新课的?这样导入有什么作用?
考题
“基本不等式”是高中数学教学中的重要内容,请完成下列任务:
(1)在“基本不等式”起始课的“教学重点”设计中,有两种方案:
①强调基本不等式在求数值中的应用,将基本不等式的应用作为重点。
②强调基本不等式的背景,过程与意义,将学生感受和体验“基本不等式”中“基本”的意义作为重点。
你赞同哪种方案?简述理由。(10分)
(3)为了让高中生充分认识“基本不等式”中“基本”的意义,作为教师应该对此有多个维度的理解,请至少从两个维度谈谈你对“基本”意义的认识。(10分)
考题
下列关于高中数学基础性的说法不正确的是( )A.高中数学课程为学生进一步学习提高了必要的数学准备
B.高中数学为不同学生提供相同的基础
C.高中数学课程体现时代性、基础性和选择性
D.高中数学课程要以学生的发展为本,尊重他们的个性发展
考题
在《普通高中数学课程标准(实验)》q-关于“二元一次不等式组与简单线性规划问题”的内容及要求如下:
①从实际情境中抽象出二元一次不等式组。
②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组。
③从实际情境中抽象出一些简单的二元线性规划问题.并能加以解决。
结合必修5“简单的线性规划问题”这一节的内容,完成下列设计。
(1)确定本节课的教学目标:
(2)确定本节课的教学重点和难点:
(3)给出本节课的教学过程。
考题
“基本不等式”是高中数学教学中的重要内容,请完成下列任务:
(1)在“基本不等式”起始课的“教学重点”设计中,有两种方案:①强调基本不等式在求数值中的应用,将基本不等式的应用作为重点。②强调基本不等式的背景,过程与意义,将学生感受和体验“基本不等式”中“基本”的意义作为教学重点。你赞同哪种方案?简述理由。(2)给出的几何解释。
(3)为了让高中生充分认识“基本不等式”中“基本”的意义,作为教师应该对此有多个维度的理解,请至少从两个维度谈谈你对“基本”意义的认识。
考题
下列关于高中数学基础性的说法不正确的是()。A、高中数学课程为学生进一步学习提供了必要的数学准备B、高中数学课程为不同学生提供相同的基础C、高中数学课程体现时代性、基础性和选择性D、高中数学课程要以学生的发展为本,尊重他们的个性发展
考题
下列关于高中数学课程结构的说法不正确的是()。A、高中数学课程可分为必修与选修两类B、高中数学选修课程包括4个系列的课程C、高中数学必修课程包括5个模块D、高中课程的组合具有固定性,不能发生改变
考题
单选题下列关于高中数学课程结构的说法不正确的是()。A
高中数学课程可分为必修与选修两类B
高中数学选修课程包括4个系列的课程C
高中数学必修课程包括5个模块D
高中课程的组合具有固定性,不能发生改变
考题
填空题在高中“不等式选讲”的教学中,应强调不等式及其证明的()与背景,以加深学生对这些不等式的数学本质的理解。
热门标签
最新试卷