网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
在有理数运算的课堂教学片段中, 某学生的板演如下:

问题:
(1) 请指出该生解题中的错误, 并分析产生错误的原因;(10 分)
(2) 针对该生在解题中的错误, 教师呈现如下两个例题, 并板书了解答过程
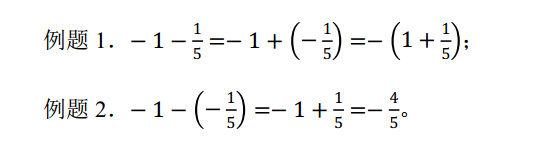
请分析例题 1、 例题 2 中每一步运算的依据。

问题:
(1) 请指出该生解题中的错误, 并分析产生错误的原因;(10 分)
(2) 针对该生在解题中的错误, 教师呈现如下两个例题, 并板书了解答过程
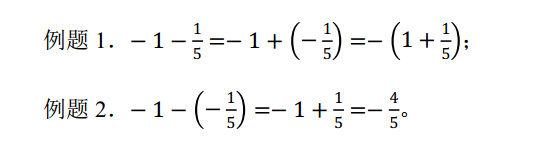
请分析例题 1、 例题 2 中每一步运算的依据。
参考答案
参考解析
解析: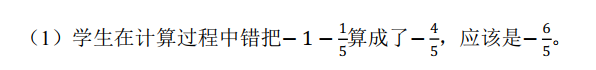
出现这样的错误,有以下几个原因:①学生没有完全理解正数和负数的概念,没能将正数、负数和相反数这些概念联系起来。②学生对于符号的认识和理解不够全面,比如数学符号“-”,除了当作减号进行运算外,还可以当作负号,表示一个数的相反数。③学生对于负数的运算法则和运算律掌握不扎实。④教师在新课讲解过程中,对学生的预设不足,对于学生难以理解的知识点,没有进行更加细致和通俗的讲解。
(2)例1是有理数的减法。第一步是利用有理数减法法则,减去一个数等于加这个数的相反数,将减法转化为加法。第二步是同号有理数加法,取相同的符号,然后把绝对值相加。
例2是有理数的减法。第一步利用有理数的减法法则,减去一个数等于加这个数的相反数,将减法转化为加法。第二步是两个异号的绝对值不相等的有理数相加,取绝对值较大数的符号,并用
较大的绝对值减去较小的绝对值。
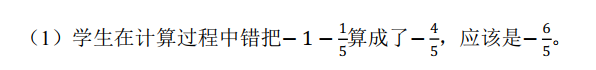
出现这样的错误,有以下几个原因:①学生没有完全理解正数和负数的概念,没能将正数、负数和相反数这些概念联系起来。②学生对于符号的认识和理解不够全面,比如数学符号“-”,除了当作减号进行运算外,还可以当作负号,表示一个数的相反数。③学生对于负数的运算法则和运算律掌握不扎实。④教师在新课讲解过程中,对学生的预设不足,对于学生难以理解的知识点,没有进行更加细致和通俗的讲解。
(2)例1是有理数的减法。第一步是利用有理数减法法则,减去一个数等于加这个数的相反数,将减法转化为加法。第二步是同号有理数加法,取相同的符号,然后把绝对值相加。
例2是有理数的减法。第一步利用有理数的减法法则,减去一个数等于加这个数的相反数,将减法转化为加法。第二步是两个异号的绝对值不相等的有理数相加,取绝对值较大数的符号,并用
较大的绝对值减去较小的绝对值。
更多 “在有理数运算的课堂教学片段中, 某学生的板演如下: 问题: (1) 请指出该生解题中的错误, 并分析产生错误的原因;(10 分) (2) 针对该生在解题中的错误, 教师呈现如下两个例题, 并板书了解答过程 请分析例题 1、 例题 2 中每一步运算的依据。” 相关考题
考题
有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24。例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)现有四个有理数3,4,-6,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24。运算式如下:(1) ,(2) ,(3) 。另有四个有理数3,-5,7,-13,可通过运算式(4) 使其结果等于24。
考题
请教:2012年七年级上册数学有理数单元测试题(含答案)第4大题第3小题如何解答?
【题目描述】
有一种二十四点的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24。例如对1,2,3,4,可作如下运算:(1+2+3)4=24(上述运算与4(1+2+3)视为相同方法的运算)
现有四个有理数3,4,-6,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24。运算式如下:(1),(2),(3)。
另有四个有理数3,-5,7,-13,可通过运算式(4)使其结果等于24。
考题
设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的,S,有*=,则S
设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的<a,b>,<x,y>S,有<a,b>*<x,y>=<ax,ay+b>,则S中关于运算*的单位元为(54)。A.<1,0>B.<0,1>C.<1,1>D.<0,0>
考题
根据题目要求完成下列任务。用中文作答。
下面是某教师的课堂教学片段:
请根据所给材料回答下列3个问题。
(1)这是课堂教学的哪一个环节?(6分)
(2)该教师使用了哪些教学手段,分别达到什么教学目的?(12分)
(3)根据这一教学片段,教师在课堂互动中应注意哪些问题?(12分)
考题
教师发现两位学生板演的内容与自己预设的内容不一致。
问题:
(1)你如何评价这两位学生的解题过程。
(2)假如你是该教师,针对学生板演的情况,如何组织进一步的教学,完成该题的教学任务。
考题
案例:
在“有理数运算”的习题课上,有这样一道题:
问题:
(1)判断学生甲、乙、丙的运算过程是否正确;(4分)
(2)请指出学生运算过程中的错误,并分析产生错误的原因;(8分)
(3)针对有理数的运算,谈谈如何提高学生的运算能力。(8分)
考题
在“三角函数求值”的教学中,教师给出来如下问题:
教师发现两位学生板书演示的内容与自己预设的内容不一致。
问题:
(1)你如何评价这两位学生的解题过程。(10分)
(2)假如你是该教师,针对学生板演的情况,如何组织进一步的教学,完成该课题的教学任务。(10分)
考题
在《有理数的加法》一节中,对于有理数加法的运算法则的形成过程,两位老师的一些教学环节分别如下:
【教师1】
第一步:教师直接给出几个有理数加法算式,引导学生根据有理数的分类标准,将加法算式分成六类,即:正数与正数相加,正数与负数相加,正数与0相加,0与0相加,负数与0相加,负数与负数相加;
第二步:教师给出具体情境,分析两个正数相加、两个负数相加、正数与负数相加的情况;
第三步:让学生进行模仿练习;
第四步:教师将学生模仿练习的题目再分成四类:同号相加,一个加数是0,互为相反数的两个数相加,异号相加。分析每一类题目的特点,得到有理数加法法则。
【教师2】
第一步:请学生列举一些有理数加法的算式;
第二步:要求学生先独立运算,然后小组讨论,再全班交流。对于讨论交流的过程,教师提出具体要求:运算的结果是什么?你是怎么得到结果的?
……讨论过程中,学生提出利用具体情境来解释运算的合理性……
第三步:教师提出问题:“不考虑具体情境,基于不同情况分析这些算式的运算有哪些规律?”
……分组讨论后再全班交流,归纳得到有理数加法法则。
问题:
(1)两位教师均重视分类讨论思想,简要说明并评价这两位教师关于分类讨论思想的教学方法的差异;
(2)请你再举两个分类讨论的例子,并结合你的例子谈谈对数学中的分类讨论思想及其教学的理解。
考题
案例:
在有理数运算的课堂教学片段中,某学生的板演如下:
针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。
请分析例题1、例题2中每一步运算的依据。(10分)
考题
中学生在学习了单项式乘多项式的有理数代数运算规则后,学习如(a+b)(a-b)多项式运算规则,根据加涅的学习结果分类,这一学习属于()。A、发现学习B、接受学习C、高级规则学习D、认知策略学习
考题
某美术教师在《文化衫的设计与制作》一课中,在进行学生作品的展示与评价时,他采用了如下评价方式:①组织学生分小组进行欣赏评价,让学生自由欣赏其他同学作品,引导学生进行自评、互评;②各组推荐优秀的作品上台,集体评价,评价出十佳优秀设计师”;③最后教师进行总体评价,及时鼓励每个有进步的学生。问题:该教学片段中的评价方式是否合适?为什么?
考题
问答题某美术教师在《文化衫的设计与制作》一课中,在进行学生作品的展示与评价时,他采用了如下评价方式:①组织学生分小组进行欣赏评价,让学生自由欣赏其他同学作品,引导学生进行自评、互评;②各组推荐优秀的作品上台,集体评价,评价出十佳优秀设计师”;③最后教师进行总体评价,及时鼓励每个有进步的学生。问题:该教学片段中的评价方式是否合适?为什么?
考题
问答题课堂教学是学生接受知识的主要途径,在信息技术教学中,课堂教学形式有哪些?
热门标签
最新试卷