网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
在《有理数的加法》一节中,对于有理数加法的运算法则的形成过程,两位老师的一些教学环节分别如下:
【教师1】
第一步:教师直接给出几个有理数加法算式,引导学生根据有理数的分类标准,将加法算式分成六类,即:正数与正数相加,正数与负数相加,正数与0相加,0与0相加,负数与0相加,负数与负数相加;
第二步:教师给出具体情境,分析两个正数相加、两个负数相加、正数与负数相加的情况;
第三步:让学生进行模仿练习;
第四步:教师将学生模仿练习的题目再分成四类:同号相加,一个加数是0,互为相反数的两个数相加,异号相加。分析每一类题目的特点,得到有理数加法法则。
【教师2】
第一步:请学生列举一些有理数加法的算式;
第二步:要求学生先独立运算,然后小组讨论,再全班交流。对于讨论交流的过程,教师提出具体要求:运算的结果是什么?你是怎么得到结果的?
……讨论过程中,学生提出利用具体情境来解释运算的合理性……
第三步:教师提出问题:“不考虑具体情境,基于不同情况分析这些算式的运算有哪些规律?”
……分组讨论后再全班交流,归纳得到有理数加法法则。
问题:
(1)两位教师均重视分类讨论思想,简要说明并评价这两位教师关于分类讨论思想的教学方法的差异;
(2)请你再举两个分类讨论的例子,并结合你的例子谈谈对数学中的分类讨论思想及其教学的理解。
【教师1】
第一步:教师直接给出几个有理数加法算式,引导学生根据有理数的分类标准,将加法算式分成六类,即:正数与正数相加,正数与负数相加,正数与0相加,0与0相加,负数与0相加,负数与负数相加;
第二步:教师给出具体情境,分析两个正数相加、两个负数相加、正数与负数相加的情况;
第三步:让学生进行模仿练习;
第四步:教师将学生模仿练习的题目再分成四类:同号相加,一个加数是0,互为相反数的两个数相加,异号相加。分析每一类题目的特点,得到有理数加法法则。
【教师2】
第一步:请学生列举一些有理数加法的算式;
第二步:要求学生先独立运算,然后小组讨论,再全班交流。对于讨论交流的过程,教师提出具体要求:运算的结果是什么?你是怎么得到结果的?
……讨论过程中,学生提出利用具体情境来解释运算的合理性……
第三步:教师提出问题:“不考虑具体情境,基于不同情况分析这些算式的运算有哪些规律?”
……分组讨论后再全班交流,归纳得到有理数加法法则。
问题:
(1)两位教师均重视分类讨论思想,简要说明并评价这两位教师关于分类讨论思想的教学方法的差异;
(2)请你再举两个分类讨论的例子,并结合你的例子谈谈对数学中的分类讨论思想及其教学的理解。
参考答案
参考解析
解析:(1)第一位老师的教学方法是典型的讲授法,从一开始便将分类的思想贯穿其中,教师直接给出几个有理数加法算式并引导学生利用以前学过的有理数的分类标准进行迁移,对有理数加法算式进行分类,能够使得学生快速地接受新知识,解决实际问题。
第二位教师在教学之初并没有强调分类的重要性,但是该教师能够以学生为主体,让学生列举一些有理数的加法的算式,充分调动了学生的主观能动性。再通过小组讨论,学生交流等过程,调动学生的学习积极性给与了充分的时间与空间,对有理数加法进行讨论计算,有助于学生发散性思维的培养。
(2)举例1:关于x的方程ax2-(a+2)x+2=0只有一解(相同解算一解),则a的值为( )。
本题的解题过程中,需要学生展开分类讨论,不仅要考虑一元二次方程两根相同的情况,还应考虑到在二次项系数为零且一次项系数不为0时的一元一次方程也同样满足题意。
举例2:解一元二次不等式x2-9>0。
解:∵x2-9=(x+3)(x-3),
∴(x+3)(x-3)>0;
由有理数的乘法法则“两数相乘,同号得正”,不等式的解共有两种情况分别是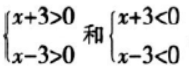 ,再对两个不等式组分别求解。
,再对两个不等式组分别求解。
分类的过程就是对事物共性的抽象过程,在教学活动中,要使学生逐步体会为什么要分类,如何分类,如何确定分类的标准,在分类过程中如何认识对象的性质,如何区别不同对象的不同性质。分类讨论是一种思想方法,需要渗透到学生的意识中,才能有效指导实践,渗透的过程不是一蹴而就的,而是需要在教学过程中,多次反复地思考和长时间的积累才能将这种思维方式不断融入知识学习的各个阶段。
第二位教师在教学之初并没有强调分类的重要性,但是该教师能够以学生为主体,让学生列举一些有理数的加法的算式,充分调动了学生的主观能动性。再通过小组讨论,学生交流等过程,调动学生的学习积极性给与了充分的时间与空间,对有理数加法进行讨论计算,有助于学生发散性思维的培养。
(2)举例1:关于x的方程ax2-(a+2)x+2=0只有一解(相同解算一解),则a的值为( )。
本题的解题过程中,需要学生展开分类讨论,不仅要考虑一元二次方程两根相同的情况,还应考虑到在二次项系数为零且一次项系数不为0时的一元一次方程也同样满足题意。
举例2:解一元二次不等式x2-9>0。
解:∵x2-9=(x+3)(x-3),
∴(x+3)(x-3)>0;
由有理数的乘法法则“两数相乘,同号得正”,不等式的解共有两种情况分别是
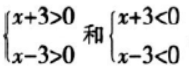 ,再对两个不等式组分别求解。
,再对两个不等式组分别求解。
分类的过程就是对事物共性的抽象过程,在教学活动中,要使学生逐步体会为什么要分类,如何分类,如何确定分类的标准,在分类过程中如何认识对象的性质,如何区别不同对象的不同性质。分类讨论是一种思想方法,需要渗透到学生的意识中,才能有效指导实践,渗透的过程不是一蹴而就的,而是需要在教学过程中,多次反复地思考和长时间的积累才能将这种思维方式不断融入知识学习的各个阶段。
更多 “在《有理数的加法》一节中,对于有理数加法的运算法则的形成过程,两位老师的一些教学环节分别如下: 【教师1】 第一步:教师直接给出几个有理数加法算式,引导学生根据有理数的分类标准,将加法算式分成六类,即:正数与正数相加,正数与负数相加,正数与0相加,0与0相加,负数与0相加,负数与负数相加; 第二步:教师给出具体情境,分析两个正数相加、两个负数相加、正数与负数相加的情况; 第三步:让学生进行模仿练习; 第四步:教师将学生模仿练习的题目再分成四类:同号相加,一个加数是0,互为相反数的两个数相加,异号相加。分析每一类题目的特点,得到有理数加法法则。 【教师2】 第一步:请学生列举一些有理数加法的算式; 第二步:要求学生先独立运算,然后小组讨论,再全班交流。对于讨论交流的过程,教师提出具体要求:运算的结果是什么?你是怎么得到结果的? ……讨论过程中,学生提出利用具体情境来解释运算的合理性…… 第三步:教师提出问题:“不考虑具体情境,基于不同情况分析这些算式的运算有哪些规律?” ……分组讨论后再全班交流,归纳得到有理数加法法则。 问题: (1)两位教师均重视分类讨论思想,简要说明并评价这两位教师关于分类讨论思想的教学方法的差异; (2)请你再举两个分类讨论的例子,并结合你的例子谈谈对数学中的分类讨论思想及其教学的理解。” 相关考题
考题
设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的,∈S,有*=,则S
设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的<a,b>,<x,y>∈S,有<a,b>*<x,y>=<ax,ay+b>,则S中关于运算*的单位元为______。A.<1,0>B.<0,1>C.<1,1>D.<0,0>A.B.C.D.
考题
设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的,S,有*=,则S
设S=Q×Q,Q为有理数集合,*为S上的二元运算,对于任意的<a,b>,<x,y>S,有<a,b>*<x,y>=<ax,ay+b>,则S中关于运算*的单位元为(54)。A.<1,0>B.<0,1>C.<1,1>D.<0,0>
考题
初中数学《有理数的减法》
一、考题回顾
二、考题解析
【教学过程】
(一)引入新课
1.两个数的和是正数,那么这两个数( )
A.都是正数 B.一正一负 C.都是负数 D.至少有一个是正数
(四)小结作业
引导学生总括:有理数减法法则是一个转化法则,减数变为它的相反数,从而减法转化为加法.可见,引进负数后对加法和减法,可以用统一的加法来解决。题目来源于考生回忆
不论是正数、负数或是零,都符合有理数减法法则,在使用法则时,注意减号变加号的同时把减数变成它的相反数,而被减数不变.
设置作业:
已知有理数a、b在数轴上对应的位置如图所示:
考题
案例:
在“有理数运算”的习题课上,有这样一道题:
问题:
(1)判断学生甲、乙、丙的运算过程是否正确;(4分)
(2)请指出学生运算过程中的错误,并分析产生错误的原因;(8分)
(3)针对有理数的运算,谈谈如何提高学生的运算能力。(8分)
考题
在学习《有理数的加法》一课时,某位教师对该课进行了深入的研究,做出了合理的教学设计,根据该课内容完成下列任务:
(1)本课的教学目标是什么
(2)本课的教学重点和难点是什么
(3)在情境引入的时候,某位老师通过一道实际生活中遇到的走路问题引出有理数的加法,让学生讨论得出有理数加法的两个数的符号,这样做的意义是什么
考题
在“有理数的加法”一节中,对于有理数加法的运算法则的形成过程,两位教师的一些教学环节分别如下:
【教师1】
第一步:教师直接给出几个有理数加法算式,引导学生根据有理数的分类标准,将加法算式分成六类,即正数与正数相加,正数与负数相加,正数与0相加,0与0相加,负数与0相加,负数与负数相加。
第二步:教师给出具体情境,分析两个正数相加,两个负数相加,正数与负数相加的情况。
第三步:让学生进行模仿练习。
第四步:教师将学生模仿练习的题目分成四类:同号相加,一个加数是0,互为相反数的两个数相加,异号相加。分析每一类题目的特点,得到有理数加法法则。
【教师2】
第一步:请学生列举一些有理数加法的算式。
第二步:要求学生先独立运算,然后小组讨论,再全班交流。对于讨论交流的过程,教师提出具体要求:运算的结果是什么?你是怎么得到结果的?
……讨论过程中,学生提出利用具体情境来解释运算的合理性……
第三步:教师提出问题:“不考虑具体情境,基于不同情况分析这些算式的运算,有哪些规律?”
……分组讨论后再全班交流,归纳得到有理数加法法则。
问题:
(1)两个教师均重视分类讨论思想,简要说明并评价这两位教师关于分类讨论思想的教学方法的差异;(8分)
(2)请你再列举两个分类讨论的例子,并结合你的例子说说对数学中的分类讨论思想及其教学的理解。(12分)
考题
在有理数运算的课堂教学片段中, 某学生的板演如下:
问题:
(1) 请指出该生解题中的错误, 并分析产生错误的原因;(10 分)
(2) 针对该生在解题中的错误, 教师呈现如下两个例题, 并板书了解答过程
请分析例题 1、 例题 2 中每一步运算的依据。
考题
案例:
在有理数运算的课堂教学片段中,某学生的板演如下:
针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。
请分析例题1、例题2中每一步运算的依据。(10分)
考题
单选题环R中的运算应该满足几条加法法则和几条乘法法则?()A
3、3B
2、2C
4、2D
2、4
热门标签
最新试卷