网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
初中数学《三角形内角和》
一、考题回顾
题目来源:5月18日 上午 吉林省通化市 面试考题
试讲题目
1.题目:三角形内角和
2.内容:
3.基本要求:
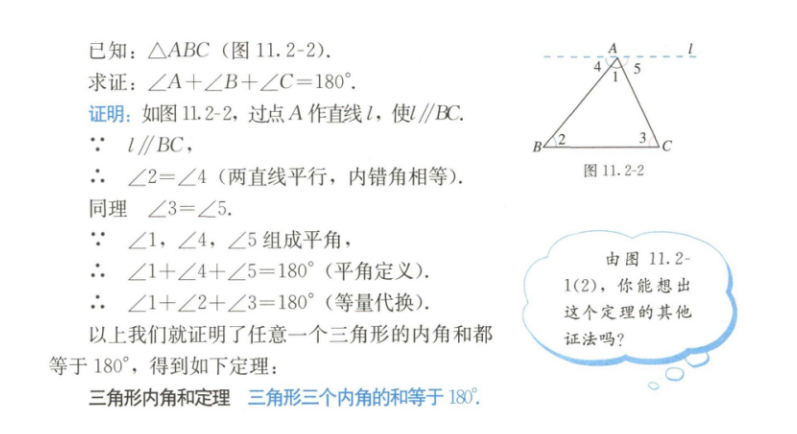
(1)能够证明三角形的内角和是180°,并解决相关问题。
(2)试讲十分钟;
(3)要有合适的板书。
答辩题目
1.在验证三角形的内角和的过程中运用了哪些教学方法?
2.本节课的在教材中的地位和作用?
一、考题回顾
题目来源:5月18日 上午 吉林省通化市 面试考题
试讲题目
1.题目:三角形内角和
2.内容:


3.基本要求:
(1)能够证明三角形的内角和是180°,并解决相关问题。
(2)试讲十分钟;
(3)要有合适的板书。
答辩题目
1.在验证三角形的内角和的过程中运用了哪些教学方法?
2.本节课的在教材中的地位和作用?
参考答案
参考解析
解析:二、考题解析
【教学过程】
(一)导入新课
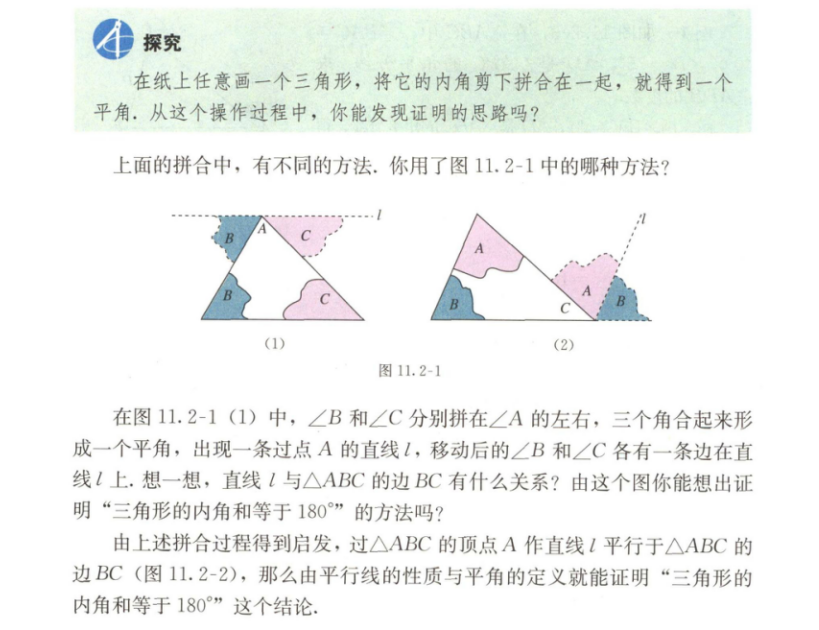
回顾小学阶段学习三角形内角和定理时,利用剪一剪、拼一拼的实验验证方法,通过复习导入引出课题。
(二)新知探索
组织学生进行小组讨论,用拼合的方法探究三角形内角和的证明思路。
引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论,再各组派代表在全班进行交流。
在交流的过程中出现了多种拼合方法,教师组织学生集体评价,并及时引导学生展开讨

【答辩题目解析】
1. 在验证三角形的内角和的过程中运用了哪些教学方法?
【参考答案】
在验证三角形的内角和的过程中运用了小组讨论和自主探究的教学方法。组织学生进行小组讨论,用拼合的方法探究三角形内角和的证明思路。引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论,再各组派代表在全班进行交流。然后让学生自主探究通利用数学方法证明三角形的内角和定理?通过这样的教学方法,可以充分体现学生的主体性。
2. 本节课的在教材中的地位和作用?
【参考答案】
本节课选自人教版初中数学八年级上册第十一章第二节内容《三角形的内角》第一课时,它是在学生掌握了三角形的特征和分类的基础上教学的。其中三角形内角和的探索和证明过程是本节课的重要教学内容。本节课的内容又是多边形内角和的基础,具有承前启后的作用。
【教学过程】
(一)导入新课
回顾小学阶段学习三角形内角和定理时,利用剪一剪、拼一拼的实验验证方法,通过复习导入引出课题。
(二)新知探索
组织学生进行小组讨论,用拼合的方法探究三角形内角和的证明思路。
引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论,再各组派代表在全班进行交流。
在交流的过程中出现了多种拼合方法,教师组织学生集体评价,并及时引导学生展开讨

【答辩题目解析】
1. 在验证三角形的内角和的过程中运用了哪些教学方法?
【参考答案】
在验证三角形的内角和的过程中运用了小组讨论和自主探究的教学方法。组织学生进行小组讨论,用拼合的方法探究三角形内角和的证明思路。引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论,再各组派代表在全班进行交流。然后让学生自主探究通利用数学方法证明三角形的内角和定理?通过这样的教学方法,可以充分体现学生的主体性。
2. 本节课的在教材中的地位和作用?
【参考答案】
本节课选自人教版初中数学八年级上册第十一章第二节内容《三角形的内角》第一课时,它是在学生掌握了三角形的特征和分类的基础上教学的。其中三角形内角和的探索和证明过程是本节课的重要教学内容。本节课的内容又是多边形内角和的基础,具有承前启后的作用。
更多 “初中数学《三角形内角和》 一、考题回顾 题目来源:5月18日 上午 吉林省通化市 面试考题 试讲题目 1.题目:三角形内角和 2.内容: 3.基本要求: (1)能够证明三角形的内角和是180°,并解决相关问题。 (2)试讲十分钟; (3)要有合适的板书。 答辩题目 1.在验证三角形的内角和的过程中运用了哪些教学方法? 2.本节课的在教材中的地位和作用?” 相关考题
考题
三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把看作它任何条件下都适用的真理。但是,19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上、三角形内角之和小于180。,随后,德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180°。这说明真理是( )。 A.因人而异的 B.具体的 C.有条件的 D.客观的
考题
如果三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各内角
如果三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各内角的度数是_____________。
考题
公元前3世纪,古希腊数学家欧几里得提出:“三角形内角之和等于180度。”19世纪德国数学家黎曼提出:“在球面上,三角形内角之和大于180度。”后来,俄国数学家罗巴切夫斯基又提出:“在凹面上,三角形内角之和小于180度。”这一认识过程说明
A.真理具有客观性
B.真理具有相对性
C.真理具有绝对性
D.真理具有唯一性
考题
在平面中三角形内角和等于180度,在球面中三角形内角和大于180度,在凹面中三角形内角和小于180度,这说明( )。A.真理具有决定性
B.真理具有相对性
C.真理具有客观性
D.真理具有全面性
考题
小学数学《三角形的内角和》
一、考题回顾
题目来源:5月18日 上午 安徽省亳州市 面试考题
试讲题目
1.题目:三角形的内角和
2.内容:
3.基本要求:
(1)注重探究过程,引导学生探究三角形的内角和;
(2)教学中注意师生间的交流互动,设置提问环节;
(3)要求配合教学内容有适当的板书设计;
(4)十分钟内结束试讲。
答辩题目
1.直角、锐角、钝角三角形是按照什么标准分类的?
2.在本节课的教学过程中,你是如何引导学生进行探究?
考题
材料一人类认识和把握世界的过程,也就是追求真理的过程。我们可以用纸折叠的方式来检验在平面上三角形内角之和等于180度,不管我们以前有没有认识到这一点,它都是不以人的意志为转移的,是客观存在的。我们实践中获得了平面上三角形内角之和等于180度的真理性的认识。
材料二我们知道了在平面上三角形内角之和等于180度。19世纪初,德国数学家指出:在球形凸面上,三角形内角之和大于180度。由此,人们关于空间的观念发生了革命性的转变。我们在地球仪上随意选择三点构成三角形直观感悟内角之和的情况。可以看到赤道、经线90度和0度经线构成270度的角。
材料三 随着农林畜牧业的发展、土地丈量和利用的增多,使人们逐渐确立了三角形内角之和等于180度的认识。随着航海事业的发展和人们对球面认识的不断深入,这一认识的局限性逐渐暴露出来。 19世纪初,俄国数学家提出:在凹曲面上,三角形内角之和小于180度。
这个过程受到了什么因素的制约?
考题
在平面中三角形内角和等于180°,但在球面中,三角形内角和大于180°,在凹面中内角和小于180°。这说明()。A、真理具有绝对性B、真理具有相对性C、真理具有客观性D、真理具有全面性
考题
单选题在平面中三角形内角和等于180°,但在球面中,三角形内角和大于180°,在凹面中内角和小于180°。这说明()。A
真理具有绝对性B
真理具有相对性C
真理具有客观性D
真理具有全面性
考题
单选题学生在小学数学课程中通过测量或拼图学习三角形的内角和为180度,在中学数学课程中通过证明学习三角形的内角和为180度。这种课程内容的组织形式是( )。A
直线式B
螺旋式C
纵向式D
横线式
考题
单选题张老师是一名小学数学教师,他想讲授三角形形状与内角和之间的变化,以下哪些描述更适合他使用()A
使用几何画板动态演示三角形变化与内角和之间的关系B
让学生在几何画板中体验三角形形状与内角和之间的关系C
提供多种三角形形状,让学生探索三角形形状与内角和之间的关系D
提供一些资源,让学生证明三角形内角和与形状间的关系
热门标签
最新试卷