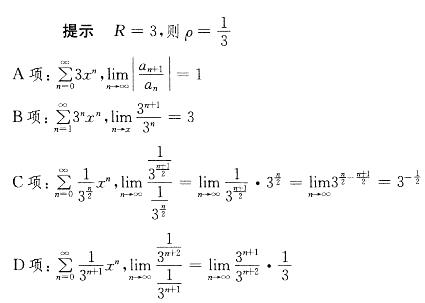
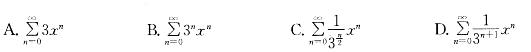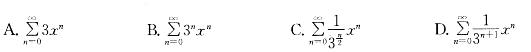考题
将函数f(x)=1/(3-x)展开成(x+1)的幂级数并指出收敛区间(6分)
考题
幂级数的收敛域是( )。A.[-2,4)
B.(-2,4)
C.(-1,1)
D.
考题
幂级数在其收敛区间的两个端点处如何敛散?
A.全是发散的 B.全是收敛的
C.左端点收敛,右端点发散 D.左端点发散,右端点收敛
考题
设幂级数的收敛区间是:
A. (-2,2)
B. (-2,4)
C. (0,4)
D. (-4,0)
考题
已知幂级数则所得级数的收敛半径R等于:
A.b D.R 值与 a、b 无关
考题
已知幂级数在x=0处收敛,在x=-4处发散,则幂级数的收敛域为________.
考题
幂级数的收敛域为()。
A. [-1,1) B. [4,6) C. [4,6] D. (4,6]
考题
设幂级数的收敛半径为2,则幂级数的收敛区间是( )。
A. (-2,2) B. (-2,4) C. (0,4) D. (-4,0)
考题
已知幂级数的收敛半径R=1,则幂级数的收敛域为( )。
A. (-1,1] B. [-1,1] C. [-1,1) D.(-∞,+∞)
考题
若幂级数在x=-2处收敛,在x = 3处发散,则该级数( )。
A.必在x = -3处发散 B.必在x=2处收敛
C.必在 x >3时发散 D.其收敛区间为[-2,3)
考题
若,则幂级数 ( )。
A.必在 x >3时发散 B.必在 x ≤3时发敛
C.在x=-3处的敛散性不定 D.其收敛半径为3
考题
将ex展开为x的幂级数,则展开式中含x3项的系数为——.
考题
将函数f(x)=xe3x展开为x的幂级数,并指出其收敛区间.
考题
设幂级数在x=2处收敛,则该级数在x=-1处必定().A.发散
B.条件收敛
C.绝对收敛
D.敛散性不能确定
考题
对于幂级数,其一般项系数开n次方后的极限为无穷大,则该幂级数发散。
考题
对级数敛散性的判别,幂级数适用于()。A、收敛B、绝对收敛C、绝对一致收敛D、点点收敛
考题
幂级数的收敛半径为2,则幂级数的收敛区间是()A、(-2,2)B、(-2,4)C、(0,4)D、(-4,0)
考题
幂级数的收敛区间为()。A、[-1,1]B、(-1,1]C、[-1,1)D、(-1,1)
考题
单选题幂级数的收敛域为()。A
[-1,1)B
[4,6)C
[4,6]D
(4,6]
考题
单选题幂级数的收敛半径为2,则幂级数的收敛区间是()A
(-2,2)B
(-2,4)C
(0,4)D
(-4,0)
考题
填空题由于高斯投影区域不大,其中()值和椭球半径相比也很小,因此可将(l,q)展开为()的幂级数。
考题
单选题知幂级数的收敛半径R=1,则幂级数的收敛域为()。A
(-1,l]B
[-1,1]C
[-1,1)D
(-∞,+∞)