考题
设平面薄板所占xOy平面上的区域D为1≤x2+y2≤4，*≥0，y≥0，其面密度为π(x，y)=x2+y2，求该薄板的质量m。
考题
D是由y2=x及y=x-2所围成的区域，则化为二次积分后的结果为：
考题
化二重积分为极坐标系下的二次积分，则等于下列哪一式？
考题
将化为极坐标系下的二次积分，其形式为下列哪一式？
考题
设圆周曲线L：x2＋y2＝1取逆时针方向，则对坐标的曲线积分
值等于（ ）。A．2π
B．－2π
C．π
D．0
考题
若D是由x=0，y=0，x2+y2=1所围成在第一象限的区域，则二重积分
等于（ ）。
考题
设D为2≤x2+y2≤2x所确定的区域，则二重积分化为极坐标系下的二次积分时等于：
考题
D是由y2=x及y=x-1所围成的区域，则化为二次积分后的结果为:
考题
(其中D:x2+y2≤1)化为极坐标系下的二次积分，其形式为下列哪一式？
考题
设二次型
(b>0),
其中二次型的矩阵A的特征值之和为1，特征值之积为-12.
(1)求a，b的值；
(2)利用正交变换将二次型f化为标准形，并写出所用的正交变换和对应的正交矩阵.
考题
将二重积分 化为极坐标形式的累次积分, 其中: D:
考题
将二重积分 化为累次积分(两种形式), 其中D给定如下: D: 由所围之区域.
考题
将二重积分 化为极坐标形式的累次积分, 其中:
考题
设二次型,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化为标准型
考题
已知，二次型的秩为2. （Ⅰ）求实数a的值； （Ⅱ）求正交变换将二次型化为标准型
考题
计算,其中Ω为z2=x2+y2，z=1所围成的立体，则正确的解法是( )。
考题
下面的哪个特效可以将画面的直角坐标系转化为极坐标系（）A、Optics CompensationB、BulgeC、Polor CoordinatesD、Ripple
考题
设C为圆周x2+y2=ax（a0），则曲线积分的值是（）．A、a2B、2a2C、3a2D、4a2
考题
设z=f（x2+y2），其中f具有二阶导数，则等于（）．A、2f’（x2+y2）B、4x2f"（x2+y2）C、2’（x2+y2）+4x2f"（x2+y2）D、2xf"（x2+y2）
考题
设D={（x，y）|1≤x2+y2≤4}，则二重积分的值是（）．A、3πB、4πC、5πD、14/3π
考题
单选题设D={（x，y）|1≤x2+y2≤4}，则二重积分的值是（）．A
3πB
4πC
5πD
14/3π
考题
单选题设z=f（x2+y2），其中f具有二阶导数，则等于（）．A
2f’（x2+y2）B
4x2f（x2+y2）C
2’（x2+y2）+4x2f（x2+y2）D
2xf（x2+y2）
考题
单选题下面的哪个特效可以将画面的直角坐标系转化为极坐标系（）A
Optics CompensationB
BulgeC
Polor CoordinatesD
Ripple
考题
单选题设C为圆周x2+y2=ax（a0），则曲线积分的值是（）．A
a2B
2a2C
3a2D
4a2
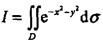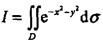(其中D：x2+y2≤1)化为极坐标系下的二次积分，其形式为( )。
。
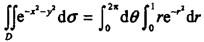
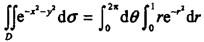