网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设f(x)为连续函数,那么 等于( )。
等于( )。
A. f(x + b) + f(x+a) B. f(x + b)-f(x + a) C. f(x+b)-f(a) D. f(b)-f(x+a)
 等于( )。
等于( )。
A. f(x + b) + f(x+a) B. f(x + b)-f(x + a) C. f(x+b)-f(a) D. f(b)-f(x+a)
参考答案
参考解析
解析: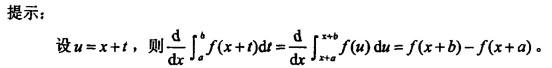
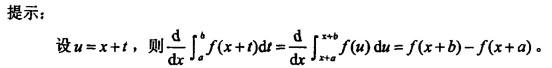
更多 “设f(x)为连续函数,那么等于( )。 A. f(x + b) + f(x+a) B. f(x + b)-f(x + a) C. f(x+b)-f(a) D. f(b)-f(x+a)” 相关考题
考题
设f(x)为连续函数,F(x)是f(x)的原函数,则( )。(A) 当f(x)是奇函数时,F(x)必为偶函数(B) 当f(x)是偶函数时,F(x)必为奇函数(C) 当f(x)是周期函数时,F(x)必为周期函数(D) 当f(x)是单增函数时,F(x)必为单增函数(E) 当f(x)是单减函数时,F(x)必为单减函数
考题
设f(x),f'(x)为已知的连续函数,则微分方程y'十f'(x)y=f(x)f'(x)的通解是:
A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +c
C. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)
考题
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0, f''(x)>0,则在(-∞,0)内必有:
A. f'(x)>0, f''(x)>0 B.f'(x)<0, f''(x)>0
C. f'(x)>0, f''(x)<0 D. f'(x)<0, f''(x)<0
考题
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上
A.A当f'(x)≥0时,f(x)≥g(x)
B.当f'(x)≥0时,f(x)≤g(x)
C.当f"(x)≥0时,f(x)≥g(x)
D.当f"(x)≥0时,f(x)≤g(x)
考题
设F1(x)与F2(x)为两个分布函数,其相应的概率密度f1(x)与f2(x)是连续函数,则必为概率密度的是
A.Af1(x)f2(x)
B.2f2(x)F1(x)
C.f1(x)F2(x)
D.f1(x)F2(x)+f2(x)f1(x)
考题
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0, f''(x)>0,则在(-∞,0)内必有:
A. f'(x)>0, f''(x)>0
B.f'(x)<0, f''(x)>0
C. f'(x)>0, f''(x)<0
D. f'(x)<0, f''(x)<0
考题
设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。
A. [f(x)/g(x)]>[f(a)/g(b)]
B. [f(x)/g(x)]>[f(b)/g(b)]
C. f(x)g(x)>f(a)g(a)
D. f(x)g(x)>f(b)g(b)
考题
设F(x)是连续函数f(x)的一个原函数,
表示“M的充分必要条件是N”,则必有( )。A.F(x)是偶函数f(x)是奇函数
B.F(x)是奇函数f(x)是偶函数
C.F(x)是周期函数f(x)是周期函数
D.F(x)是单调函数f(x)是单调函数
考题
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().
A.F(z)=F(-x)
B.F(x)=F(-x)
C.F(X)=F(-x)
D.f(x)=f(-x)
考题
不定积分∫xf(x)dx等于( )。
A. xf(x)-f(x) + C B. xf(x)-f(x) + C
C. xf(x) + f(x) + C D. xf(x) +f(x)+ C
考题
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0,f''(x)>0,则在(-∞,0)内必有( )。
A. f'(x)>0,f''(x)>0 B. f(x) 0
C. f'(x)>0,f''(x)
考题
设f(x)是连续函数,F(x)是f(x)的原函数,则()。
A.当f(x)是奇函数时,F(x)必是偶函数
B.当f(x)是偶函数时,F(x)必是奇函数
C.当f(x)是周期函数时,F(x)必是周期函数
D.当f(x)是单调增函数时,F(x)必是单调增函数
考题
设F1(x)与F2(x)为两个分布函数,其相应的概率密度f1(x)与f2(x)是连续函数,则必为概率密度的是()A、f1(x)f2(x)B、2f2(x)F1(x)C、f1(x)F2(x)D、f1(x)F2(x)+f2(x)F1(x)
考题
若f(x)的常数项a0=±1,令g(x)=f(x+b),b=1或-1,如果g(x)在Q上不可约那么可以的什么结论?()A、g(f(x))在Q不可约B、f(x)在Q不可约C、f(g(x))在Q不可约D、f(g(x+b))在Q不可约
热门标签
最新试卷