网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
如图5-20所示，为直角三角形ABD斜边上的中点，y，z轴为过中点O且分别平行于两条直角边的两根轴，关于惯性积和惯性矩为（）。

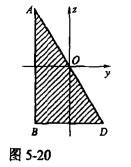
A.Iyz>0 B.Iyzyz=0 D. Iy=Iz

参考答案

参考解析
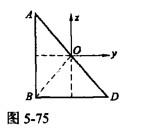
解析：提示：如图5-75所示，作辅助线OB , y轴是三角形AOB 的对称轴，z轴是三角形OBD的对称轴。
更多 “如图5-20所示，为直角三角形ABD斜边上的中点，y，z轴为过中点O且分别平行于两条直角边的两根轴，关于惯性积和惯性矩为（）。 A.Iyz>0 B.Iyzyz=0 D. Iy=Iz” 相关考题
考题 如图所示正方形截面对y1轴的惯性矩应为：
查看答案
考题 如图所示正方形截面对z1轴的惯性矩与对z轴惯性矩的关系是：
查看答案
考题 如图所示，截面面积为A，形心为C，对z轴的惯性矩为Iz，则截面对z1轴的惯性矩IZ1为（　　）。
查看答案
考题 矩形截面挖去一个边长为a的正方形，如图所示，该截面对z轴的惯性矩Iz为：
查看答案
考题 图示截面对z轴的惯性矩Iz为（　　）。
查看答案
考题 对如图所示平面图形来说，下列结论中错误的是： A. Izy=0 B. y轴和z轴均为形心主惯性轴 C. y轴是形心主惯性轴，z轴不是形心主惯性轴 D.y轴和z轴均是主惯性轴
查看答案
考题 如图所示一矩形截面，面积为A，高度为b，对称轴为z，z1和z2均平行于z，下列计算式中正确的为：
查看答案
考题 如图11所示空心矩形截面对形心轴xc轴的惯性矩为( )。
查看答案
考题 面积相等的两个图形分别如图a)和图b)所示。它们对对称轴轴的惯性矩之间的关系为：
查看答案
考题 欲使通过矩形截面长边中点O的任意轴y0为惯性轴，则矩形截面的高与宽的关系为( )。
查看答案
考题 在yOz正交坐标系中，设图形对：y、z轴的惯性矩分别为Iy和Iz，则图形对坐标原点的极惯性矩为：
查看答案
考题 面积相等的两个图形分别如图a)和图b)所示。它们对对称轴y、z轴的惯性矩之间关系为：
查看答案
考题 矩形截而挖去一个边长为a的正方形，如图所示，该截面对Z轴的惯性矩IZ为
查看答案
考题 在yoz正交坐标系中，设图形对y,z轴的惯性矩分别为Iy和Iz，则图形对坐标原点极惯性矩为：
查看答案
考题 面积相等的两个图形分别如图（a）、图（b）所示，它们对对称轴y、z 轴的惯性矩之间的关系为：
查看答案
考题 已知平面图形的形心为C，面积为A，对Z轴的惯性矩为IZ，则图形对Z1轴的惯性矩为( )。
查看答案
考题 如图所示，梯形ABCD的两条对角线AD、BC相交于O，EF平行于两条边且过O点。现已知AB=6，CD=18。问EF的长度为多少？ A. 8.5 B. 9 C. 9.5 D. 10
查看答案
考题 如图所示正方形截面对z1轴的惯性矩与对z轴的惯性矩的关系为( )。
查看答案
考题 如图5-17所示，已知平面图形的形心为C,面积为A,对z轴的惯性矩为Iz,对图形z1轴的惯性矩有四种答案为（ ）。 A. Iz + b2A B. Iz +(a + b)2 A C. Iz + (a2 -b2)A D. Iz+(b2 -a2)A
查看答案
考题 在正交坐标系中，设平面图形对y轴和z轴的惯性矩分别为Iy和Iz，则图形对坐标原点的极惯性矩为Ip=Iy2+Iz2。
查看答案
热门标签
最新试卷