网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
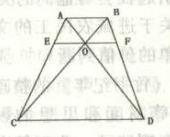
如图所示,梯形ABCD的两条对角线AD、BC相交于O,EF平行于两条边且过O点。现已知AB=6,CD=18。问EF的长度为多少?

A. 8.5
B. 9
C. 9.5
D. 10
B. 9
C. 9.5
D. 10
参考答案
参考解析
解析:解题指导: 18*BF/BD=6*DF/BD, BF/DF=1:3, OF/CD=1:4, OE/CD=1:4, EF=CD/2=9,故答案为B。
更多 “如图所示,梯形ABCD的两条对角线AD、BC相交于O,EF平行于两条边且过O点。现已知AB=6,CD=18。问EF的长度为多少? A. 8.5 B. 9 C. 9.5 D. 10 ” 相关考题
考题
已知a= "ab",那么执行语句b="cd'" & a & " " & "ef"后,变量b的值是()?
A."cd'ab ef"B."cd'abef"C."cdabef"D."cdab ef"
考题
在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
考题
六边形ABCDEF中,AB∥ED,AF∥CD,BC∥FE,且AB=ED,AF=CD,BC=EF。又FD⊥BD,FD=24cm,BD=18cm,则六边形ABCDEF的面积为()。A.432cm2B.368cm2C.216cm2D.以上A、B、C均不正确
考题
对边相等,对角相等的凸四边形,是平行四边形吧?
方法①∠B小于90°;左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:过A作AN⊥BC于N;过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法②∠B大于90°左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:延长CD,过A作AN⊥BC于N;延长AB,过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法③∠B等于90°证明:∵∠B=∠D=90°;AB=CD;AC=AC∴△ABC=△ADC(HL)∴AB=CB∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。有错吗?若我的证明有错请明示,我知道有个反例,但它是凹四边形。
考题
如图所示,一个小区的道路围成了一个五边形,经实地勘测,五边形内有三个角为直角,AD 边、BC 边和 CD 边长度相等,且 OA 边长度为其一半。 已知 AD 边长 20 米,问道路围成的五边形面积为多少
考题
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.
考题
如右图,在梯形ABCD中,点E、F分别是腰AB、CD上的点.
(1)证明:如果E、F为中点时,有 EF=1/2(AD+BC);
(2)请写出(1)中命题的逆命题,并判断该逆命题是否成立,若成立,请给予证明;若不成立,请说明理由.
考题
如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切与点C,AD⊥EF,垂足为D。
(1)若 ∠DAC=63°,求∠BAC;(5分)
(2)若把直线EF向上平行移动,如图,直线EF交 ⊙O于G和C两点,若题中的其他条件不变,这时与∠DAC相等的角是哪一个 为什么 (5分)
考题
如图所示,梯形ABCD,AD∥BC,DE⊥BC,现在假设AD、BC的长度都减少10%,DE的长度增加10%,则新梯形的面积与原梯形的面积相比,会怎样变化?
A. 不变
B. 减少1%
C. 增加10%
D. 减少10%
考题
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。
考题
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。
A.1
B.2
C.3
D.4
考题
铰链四杆机构ABCD,如果以BC为机架(静件),当机构为双曲柄机构时,各杆的长度可为()。A、AB=130 BC=150 CD=175 AD=200B、AB=150 BC=130 CD=165 AD=200C、AB=175 BC=130 CD=185 AD=200D、AB=200 BC=150 CD=165 AD=130
热门标签
最新试卷