网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设随机变量x的分布函数为
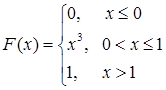
则数学期望E(X)等于( )。
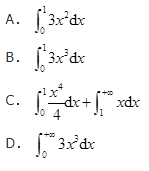
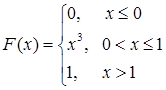
则数学期望E(X)等于( )。
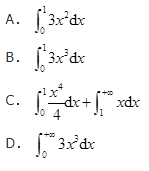
参考答案
参考解析
解析:

更多 “设随机变量x的分布函数为 则数学期望E(X)等于( )。 ” 相关考题
考题
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().
A.F(z)=F(-x)
B.F(x)=F(-x)
C.F(X)=F(-x)
D.f(x)=f(-x)
考题
设X1,X2,…,Xn,…相互独立,则X1,X2,…,Xn,…满足辛钦大数定律的条件是( )
A.X1,X2,…,Xn,…同分布且有相同的数学期望与方差
B.X1,X2,…,Xn,…同分布且有相同的数学期望
C.X1,X2,…,Xn,…为同分布的离散型随机变量
D.X1,X2,…,Xn,…为同分布的连续型随机变量
考题
多选题数学期望的性质包括()A设c为常数,则E(c)=cB设X为随机变量,α为常数,则E(αX)=αE(X)C设X、y是两个随机变量,则E(X±Y)=E(X)+E(Y)D设X、y是相互独立的随机变量,则E(XY)=E(X)E(Y)E设c为常数,则E(c)=0。
热门标签
最新试卷