网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
当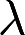 取何值时,方程组
取何值时,方程组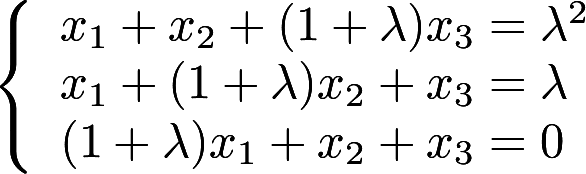 有唯一解,无解,有无穷多解?并在有无穷多解时求其通解。
有唯一解,无解,有无穷多解?并在有无穷多解时求其通解。
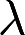 取何值时,方程组
取何值时,方程组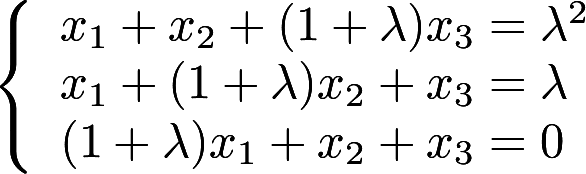 有唯一解,无解,有无穷多解?并在有无穷多解时求其通解。
有唯一解,无解,有无穷多解?并在有无穷多解时求其通解。参考答案
参考解析
解析:



更多 “当取何值时,方程组有唯一解,无解,有无穷多解?并在有无穷多解时求其通解。” 相关考题
考题
下面对线性规划解的讨论中,叙述正确的选项是( )
A.线性规划问题求解的结果有四种,它们分别是唯一解、无穷多解、无解和无界解。B.线性规划问题求解的结果有四种,它们分别是唯一解、无穷多解和无界解。C.线性规划问题求解的结果有三种,它们分别是唯一解、无穷多解、无解。D.以上说法都不正确。
考题
对方程组Ax=b与其导出组Ax=o,下列命题正确的是()。
A、Ax=o有解时,Ax=b必有解.B、Ax=o有无穷多解时,Ax=b有无穷多解.C、Ax=b无解时,Ax=o也无解.D、Ax=b有惟一解时,Ax=o只有零解.
考题
设非齐次线性方程组( I )的导出方程组为(II),则()。
A.当(I )只有唯一 解时,(II)只有零解
B. (I )有解的充分必要条件是(II)有解
C.当(I )有非零解时,(II)有无穷多解
D.当(I)有非零解时,(I )有无穷多解
考题
非齐次线性方程组AX=b中未知数个数为n,方程个数为m,系数矩阵A的秩为r,则( ).A.r=m时,方程组AX=b有解
B.r=n时,方程组AX=b有唯一解
C.m=m时,方程组AX=b有唯一解
D.r<n时,方程组AX=b有无穷多解
考题
单选题设A是m×n矩阵,AX(→)=0(→)是AX(→)=b(→)的导出组,则下列结论正确的是( )。A
若AX(→)=0(→)仅有零解,则AX(→)=b(→)有唯一解B
若AX(→)=0(→)有非零解,则AX(→)=b(→)有无穷多解C
若AX(→)=b(→)有无穷多解,则AX(→)=0(→)仅有零解D
若AX(→)=b(→)有无穷多解,则AX(→)=0(→)有非零解
考题
单选题非齐次线性方程组AX(→)=b(→)中未知数个数为n,方程个数为m,系数矩阵A的秩为r,则( )。A
r=m时,方程组AX(→)=b(→)有解B
r=n时,方程组AX(→)=b(→)有唯一解C
m=n时,方程组AX(→)=b(→)有唯一解D
r<n时,方程组AX(→)=b(→)有无穷多解
热门标签
最新试卷