网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
甲从1、2、3中抽取一个数，记为a；乙从1、2、3、4中抽取一个数，记为b，规定当a大于b或者a+1小于b时甲获胜，则甲取胜的概率为（ ）

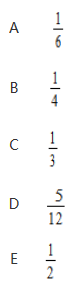
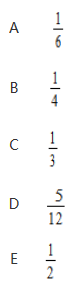
参考答案

参考解析
解析：穷举法：满足a大于b的有（2,1）（3,1）（3,2）；满足a+1小于b的有（1,3）（1,4）（2,4）；共六组，因此概率为3/6=1/2
更多 “甲从1、2、3中抽取一个数，记为a；乙从1、2、3、4中抽取一个数，记为b，规定当a大于b或者a+1小于b时甲获胜，则甲取胜的概率为（ ） ” 相关考题
考题 （本小题满分12分）（注意：在试题卷上作答无效）甲、乙二人进行一次围棋比赛，约定先胜3局者获得这次比赛的胜利，比赛结束。假设在一局中，甲获胜的概率为0.6，乙获胜的概率为0.4，各局比赛结果相互独立。已知前2局中，甲、乙各胜1局。（Ⅰ）求再赛2局结束这次比赛的概率；
查看答案
考题 从0,1,2…,9十个数字中随机地、有放回地接连抽取四个数字，则“8”至少出现一次的概率为A、0.1B、0.3439C、0.4D、0.6561
查看答案
考题 有若干个数，第一个数记为a1，第二个数记为a2，…，第n个数记为an。若a1=1/2，从第二个数起，每个数都等于“1与它前面那个数的差的倒数”。试计算：a2=______，a3=____，a4=_____，a5=______。这排数有什么规律吗？由你发现的规律，请计算a2004是多少？
查看答案
考题 有10件产品，其中8件是正品，2件是次品．甲、乙两人先后各抽取1件产品， 求甲先抽到正品的条件下，乙抽到正品的概率．
查看答案
考题 一副卡牌上面写着1到10的数字，甲和乙从中分别随机抽取三张牌，并比较其中较大的两张牌的牌面之积，数字大的人获胜。甲先抽出三张牌，上面的数字分别是2、6和8，问乙从剩下的牌中抽取三张牌的话，其胜过甲的概率（ ）A. 高于60% B. 在50%60%之间 C. 在40%50%之间 D. 低于40%
查看答案
考题 甲、乙两人同时从同一地点出发沿同一环形跑道进行健身锻炼，甲跑步，乙走路。若甲追上乙所需时间是两人相向而行相遇所需时间的3倍，则甲、乙的速度之比是：A.3︰1 B.5︰2 C.2︰1 D.3︰2
查看答案
考题 某六西格玛团队通过界定项目过程的输出，明确了缺陷的机会是甲、乙、丙。经过调查统计2个月的数据，结果在抽取的200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则该过程的DPMO为（ ）。 A. 10 000 B. 30 000 C. 60 000 D. 600
查看答案
考题 若某单位从5位优秀毕业生甲、乙、丙、丁、戊中录用三人，这五人被录用的机会均等，则甲、乙中至少一人被录用的概率为()。 A.2/3 B.1/3 C.3/5 D.9/10
查看答案
考题 甲、乙两人从1,2,…,15中各取一个数,设甲取到的数是5的倍数,求甲数大于乙数的概率.
查看答案
考题 从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？A. 10% B. 30% C. 60% D. 90%
查看答案
考题 甲、乙、丙、丁4个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这4个队分成两个组（每组两个队）进行比赛,胜者再赛,则甲、乙相遇的概率为（ ）A.1/6 B.1/4 C.1/5 D.1/3 E.1/2
查看答案
考题 从1,2,…,9这九个数中,随机抽取3个不同的数,这3个数的和为偶数的取法有（ ）种A.36 B.44 C.60 D.72 E.90
查看答案
考题 在分别记了数字1、2、3、4、5、6的6张卡片中，甲随机抽取1张后，乙从余下的卡片中再随机抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为（ ）
查看答案
考题 甲、乙依次轮流投掷一枚均匀硬币,若先投出正面者为胜,则甲获胜的概卒是（ ）A.2/3 B.1/3 C.1/2 D.1/4 E.3/4
查看答案
考题 信封中装有10张奖券，只有1张有奖．从信封中同时抽取2张奖券，中奖的概率记为P；从信封中每次抽取1张奖券后放回，如此重复抽取n次，中奖的概率记为Q．则PA.条件（1）充分，但条件（2）不充分； B.条件（2）充分，但条件（1）不充分； C.条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分； D.条件（1）充分，条件（2）也充分； E.条件（1）和条件（2）单独都不充分，条件（1）和条件（3）联合起来也不充分．
查看答案
考题 从1、2、3、4、5这五个数字中等可能地、有放回地接连抽取两个数字，则这两个数字不相同的概率为()
查看答案
考题 甲、乙两人进行五子棋比赛，必须要经过A、B、C三场比赛的角逐，甲对乙每局获胜的概率 为60%，乙对甲每局获胜的概率为40%，则甲胜出的可能性为（ ）。 A.小于15% B.介于15%--40%内 C.介于40%--60%内 D.大于60%
查看答案
考题 为研究7至10岁少年儿童的身高情况,甲、乙两名研究人员分别随机抽取了某城市100名和1000名两组调查样本,若甲、乙抽取的两组样本平均身高分别记为(单位:cm),则和的大小关系为( )A.α>β B.α＜β C.α=β D.不能确定
查看答案
考题 为研究7至10岁少年儿童的身高情况，甲、乙两名研究人员分别随机抽取了某城市100名和1 000名两组调查样本，若甲、乙抽取的两组样本平均身高分别记为d(单位：cm)，则a和β的大小关系为( )。 A． B． C． D．不能确定
查看答案
考题 为研究7至10岁少年儿童的身高情况，甲、乙两名研究人员分别随机抽取了某城市100名和1000名两组调查样本，若甲、乙抽取的两组样本平均身高分别记为、 (单位:cm)则 的大小关系为（ ）。
查看答案
考题 在区间[0，1]中随机抽取两个数(χ，y)，即(χ，y)服从[0，1]上的均匀分布。求这两个数之差的绝对值小于1/2的概率。
查看答案
考题 在0，1，2，3，4，5，6，7，8，9中随机抽取一个数字，设A为抽取的数字≤5，则P（A）=（）。
查看答案
考题 甲、乙两人随意入住两间房，则甲、乙两人住同一间房的概率是（）。A、1/4B、1/2C、2/3D、1/3
查看答案
考题 某六西格玛团队，界定项目过程的输出时，明确缺陷的机会是甲、乙、丙，经过调查统计2个月的数据，结果是在抽样200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则DPMO为（）A、60000B、30000C、10000D、600
查看答案
考题 单选题某六西格玛团队，界定项目过程的输出时，明确缺陷的机会是甲、乙、丙，经过调查统计2个月的数据，结果是在抽样200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则DPMO为（）A 60000B 30000C 10000D 600
查看答案
考题 单选题30.将0，1，2，…，9等10个数字中随机地、有放回地接连抽取4个数字，则“8”至少出现一次的概率为 A 0.1B 0.3439C 0.4D 0.6561
查看答案
考题 单选题甲、乙两人轮流投篮，每人每次投一球。约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球3次时投篮结束。设甲每次投篮投中的概率为1/3，乙每次投篮投中的概率为1/2，且各次投篮互不影响。则投篮结束时乙只投了两个球的概率为：A 1/27B 1/9C 4/27D 13/27
查看答案
热门标签
最新试卷