网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
微分方程xy’+y(lnx-lny)=0满足条件y(1)=e^3的解为y=________.
参考答案
参考解析
解析: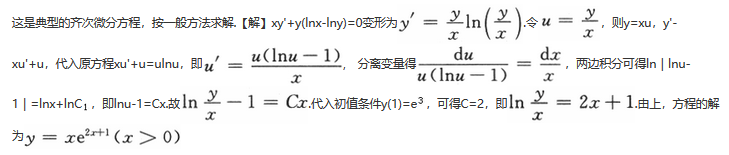
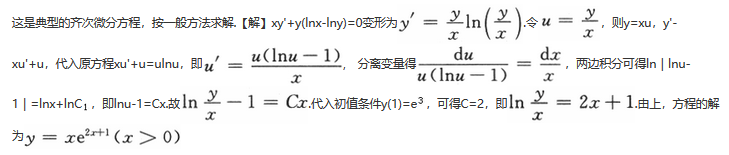
更多 “微分方程xy’+y(lnx-lny)=0满足条件y(1)=e^3的解为y=________.” 相关考题
考题
在下列微分方程中,以函数y=C1e^-x+C2e^4x(C1,C2为任意常数)为通解的微分方程是( )。A. y″+3y′-4y=0
B. y″-3y′-4y=0
C. y″+3y′+4y=0
D. y″+y′-4y=0
考题
若二阶常系数线性齐次微分方程y"+ay'+by=0的通解为y=(C1+C2x)e^x,则非齐次方程y"+ay'+by=x满足条件y(0)=2,y'(0)=0的解为y=________.
考题
曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的二倍减去2,其中x1,y0。曲线y=f(x)所满足的微分方程应是:()A、y3=2(y-xy′)B、2xy′=2yC、2xy′=-y3D、2xy=2y+y3
考题
单选题若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=( )。A
xex+x2+2B
-xex+x2+2C
-xex+x+2D
-xex+x
考题
单选题曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的二倍减去2,其中x1,y0。曲线y=f(x)所满足的微分方程应是:()A
y3=2(y-xy′)B
2xy′=2yC
2xy′=-y3D
2xy=2y+y3
考题
填空题微分方程y′=ex+y满足条件y(0)=0的特解为____。
热门标签
最新试卷