网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
微分方程y''+ay'2=0满足条件y x=0=0,y' x=0=-1的特解是:


参考答案
参考解析
解析:提示:本题为可降阶的高阶微分方程,按不显含变量x计算。设y'= P,y''=p',方程化为
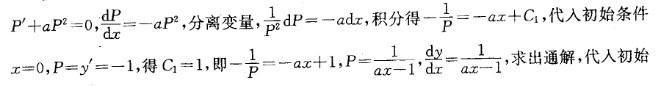
条件,求出特解。
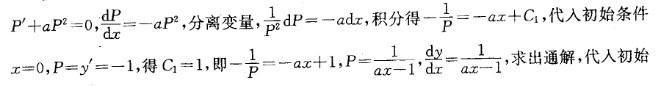
条件,求出特解。
更多 “微分方程y''+ay'2=0满足条件y x=0=0,y' x=0=-1的特解是: ” 相关考题
考题
微分方程cosydx+(1+e-x)sinydy=0满足初始条件y x=0=的特解是:
(A)cosy=(1+ex) (B)cosy=(1+ex) (C)cosy=4(1+ex) (D)cos2y=(1+ex)
考题
若二阶常系数线性齐次微分方程y"+ay'+by=0的通解为y=(C1+C2x)e^x,则非齐次方程y"+ay'+by=x满足条件y(0)=2,y'(0)=0的解为y=________.
考题
单选题(2012)已知微分方程y′+p+(x)y=q(x)[q(x)≠0]有两个不同的特解y1(x),y2(x),则该微分方程的通解是:(c为任意常数)()A
y=c(y1-y2)B
y=c(y1+y2)C
y=y1+c(y1+y2)D
y=y1+c(y1-y2)
考题
单选题若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=( )。A
xex+x2+2B
-xex+x2+2C
-xex+x+2D
-xex+x
考题
单选题具有特解y1=e-x,y2=2xe-x,y3=3ex的三阶常系数齐次线性方程是( )。A
y‴-y″-y′+y=0B
y‴+y″-y′-y=0C
y‴-6y″+11y′-6y=0D
y‴-2y″-y′+2y=0
考题
单选题以y1=ex,y2=e-3x为特解的二阶线性常系数齐次微分方程是( )。[2012年真题]A
y″-2y′-3y=0B
y″+2y′-3y=0C
y″-3y′+2y=0D
y″-2y′-3y=0
考题
单选题(2012)以y1=ex,y2=e-3x为特解的二阶线性常系数齐次微分方程是:()A
y″-2y′-3y=0B
y″+2y′-3y=0C
y″-3y′+2y=0D
y″+2y′+y=0
考题
单选题函数y1(x)、y2(x)是微分方程y′+p(x)y=0的两个不同特解,则该方程的通解为( )。A
y=c1y1+c2y2B
y=y1+cy2C
y=y1+c(y1+y2)D
y=c(y1-y2)
考题
单选题若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=( )。A
xex+x+2B
xex-x+2C
-xex-x+2D
-xex+x+2
考题
单选题微分方程y″-2y′+y=0的两个线性无关的特解是( )。[2016年真题]A
y1=x,y2=exB
y1=e-x,y2=exC
y1=e-x,y2=xe-xD
y1=ex,y2=xex
考题
单选题微分方程cosydx+(1+e-x)sinydy=0满足初始条件y|x=0=π/3的特解是( )。A
cosy=(1+ex)/4B
cosy=1+exC
cosy=4(1+ex)D
cos2y=1+ex
考题
单选题微分方程xy′-ylny=0满足y(1)=e的特解是( )。[2013年真题]A
y=exB
y=exC
y=e2xD
y=ln x
热门标签
最新试卷