网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
函数f（x）＝ax（a＞0，a≠1）的麦克劳林展开式中的前三项是（　　）。


A． 1＋xlna＋x^2/2
B． 1＋xlna＋x^2lna/2
C． 1＋xlna＋（lna）^2x^2/2
D． 1＋x/lna＋x^2/（2lna）

参考答案

参考解析
解析：麦克劳林公式是泰勒公式（在x0＝0下）的一种特殊形式。函数f（x）麦克劳林展开式为



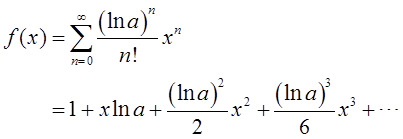
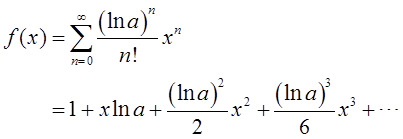
因此前三项是1＋xlna＋（lna）^2x^2/2。
更多 “函数f（x）＝ax（a＞0，a≠1）的麦克劳林展开式中的前三项是（　　）。 A． 1＋xlna＋x^2/2 B． 1＋xlna＋x^2lna/2 C． 1＋xlna＋（lna）^2x^2/2 D． 1＋x/lna＋x^2/（2lna）” 相关考题
考题 设函数f(x)的定义域是(0,1),那么f(x＋1)的定义域是()。 A.(0，1)B.(-1，0)C.(1，2)D.(0，2)
查看答案
考题 已知函数 x(t)的傅里叶变换为 X(f),则函数 y(t)=2x(t)的傅里叶变换为( )。 A. 2X(t)B. X(t )C. X(f)D. 2X(f)
查看答案
考题 已知函数f(x)=(a+1)lnx+ax2+1.(Ⅰ)讨论函数f(x)的单调性；(Ⅱ)设a≤-2，证明：对任意x2,x2 (0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|.
查看答案
考题 设函数当定义f(0)为何值时，则f(x)在x=0处连续？ A. e2 B. e C. e-2 D. e-1/2
查看答案
考题 设f(x)是连续函数， 则f(x)= A. x2 B. x2-2 C 2x D. x2 -16/9
查看答案
考题 L 是区域D:x2+y≤-2x 的正向周界， A. 2π B. 0 C.(3/2)π D. -2π
查看答案
考题 D 域由 x 轴，x2 + y2 ? 2x = 0( y ≥ 0)及 x+y=2 所围成， f (x, y)是连续函数，化
查看答案
考题 已知函数f(x)=（1/2）e2x-ax，g(x)=6xlnx，，h(x)=2e2x-4/x，a>o，b≠0。 (1)求函数f(x)的最小值；(3分) (2)求函数g(x)的单调区间；(3分) (3)证明：函数h(x)在[1/2，1]上有且仅有l个零点。(4分)
查看答案
考题 设函数f（x）=2ax2-ax，且f（2）=-6，则a=（　　）A.-1 B.0 C.1 D.4
查看答案
考题 下列函数中，为偶函数的是（）A.y=1/2x B.y=2x C.y=log2x D.y=2cosx
查看答案
考题 A． f″（x^2y） B． f′（x^2y）＋x^2f″（x^2y） C． 2x[f′（x^2y）＋yf″（x^2y）] D． 2x[f′（x^2y）＋x^2yf″（x^2y）]
查看答案
考题 若x＝1是函数y＝2x^2＋ax＋1的驻点，则常数a等于（　　）。 A． 2 B． －2 C． 4 D． －4
查看答案
考题 函数f（x）＝ax（a＞0，a≠1）的麦克劳林展开式中的前三项是（　　）。 A． 1＋xlna＋x^2/2 B． 1＋xlna＋x^2lna/2 C． 1＋xlna＋（lna）^2x^2/2 D． 1＋x/lna＋x^2/（2lna）
查看答案
考题 求函数．f(x)＝x2?2x在x=0处的n阶导数,f(n)(O)。
查看答案
考题 函数f(x)=2x+3x的零点所在的一个区间是( ) A.(-2，-l) B.(-1，0) C.(0，1) D.(1，2)
查看答案
考题 若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则的值为()。 A. 0 B. 1 C. 2 D.不存在
查看答案
考题 设f(x)是连续函数，且，则f(x)=( )。 A. x2 B. X2-2 C. 2x D. x2-16/9
查看答案
考题 函数f(x)=2x+3x的零点所在的一个区间是( )。A.(-2，-1) B.(0，1) C.(-1，0) D.(1，2)
查看答案
考题 已知函数x（t）的傅里叶变换为X（f），则函数y（t）=2x（3t）的傅里叶变换为（）A、2X（f/3）B、2/3X（f/3）C、2/3X（f）D、2X（f）
查看答案
考题 设4／（1-x2）·f（x）=d／dx［f（x）］2，且f（0）=0，则f（x）等于：（）A、（1+x）／（1-x）+cB、（1-x）／（1+x）+cC、1n｜（1+x）／（1-x）｜+cD、1n｜（1-x）／（1+x）｜+c
查看答案
考题 设a0，则当满足条件（）时，函数f（x）=ax3+3ax2+8为增函数。A、x-2B、-2C、x0D、x-2或x0
查看答案
考题 单选题y＝2x的麦克劳林公式中xn项的系数是（　　）。A （ln2）n＋1/（n！）B （ln2）n/（n！）C （ln2）n/（（n＋1）！）D （ln2）n＋1/（（n＋1）！）
查看答案
考题 单选题设4／（1-x2）·f（x）=d／dx［f（x）］2，且f（0）=0，则f（x）等于：（）A （1+x）／（1-x）+cB （1-x）／（1+x）+cC 1n｜（1+x）／（1-x）｜+cD 1n｜（1-x）／（1+x）｜+c
查看答案
考题 单选题若f′（x）为连续函数，则∫f′（2x）dx＝（　　）。A f（2x）＋CB f（x）＋CC f（2x）/2＋CD 2f（2x）＋C
查看答案
考题 单选题设a0，则当满足条件（）时，函数f（x）=ax3+3ax2+8为增函数。A x-2B -2C x0D x-2或x0
查看答案
考题 填空题y＝2x的麦克劳林公式中xn项的系数是____。
查看答案
考题 单选题y＝2x的麦克劳林公式中xn项的系数是（　　）。A 1B 2！C （ln2）n/（n！）D －（ln2）n/（n！）
查看答案
考题 单选题y＝2x的麦克劳林公式中xn项的系数是（　　）。A ln2/（n！）B （ln2）n/（n－1）！C （ln2）n/（n！）D ln2/（n－1）！
查看答案
热门标签
最新试卷