网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
向量( )是单位向量。
A.(1,1,-1)
B.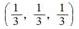
C.(-1,0,0)
D.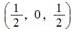
B.
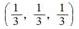
C.(-1,0,0)
D.
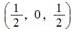
参考答案
参考解析
解析:

更多 “向量( )是单位向量。A.(1,1,-1) B. C.(-1,0,0) D.” 相关考题
考题
高中数学《空间向量》
二、考题解析
【教学过程】
(一)引入课题
(课件)引入:有一块质地均匀的正三角形面的钢板,重500千克,顶点处用与对边成60度角,大小200千克的三个力去拉三角形钢板,问钢板在这些力的作用下将如何运动?这三个力至少多大时,才能提起这块钢板?
提问:我们研究的问题是三个力的问题,力在数学中可以看成是什么?这三个向量和以前我们学过的向量有什么不同?
(学生得出:这是三个向量不共面)
追问:不共面的向量问题能直接用平面向量来解决么?解决这类问题需要空间向量的知识。这节课我们就来学习空间向量。
(二)探求新知
1.生活实例感知
空间向量我们随处可见,同学们能不能举出一些例子?(学生举例)
再演示(课件)几种常见的空间向量身影。(常见的高压电线及支架所在向量,长方体中的三个不共线的边上的向量,平行六面体中的不共线向量)
2.类比概念形成
接下来我们我们就来研究空间向量的知识、概念和特点,空间向量与平面向量既有联系又有区别,我们将通过类比的方法来研究空间向量,首先我们复习回顾一下平面向量的知识。师生一起回忆平面向量概念、向量的模、零向量、单位向量、相反向量、相等向量等,引导学生理解空间向量就是把向量放到空间中了,请同学们给空间向量下个定义,
(学生:在空间中,既有大小又有方向的量)
现在请同学们阅读教材,找出空间向量的相关定义,用类比的方法记忆并填写课件的表格:
3.类比运算定律形成
在数学中引入一种量以后,一个很自然的问题就是研究它们的运算,空间向量的运算我们也采用与平面向量类比的方法,那么我们首先来复习回顾一下平面向量的加减运算。(课件)复习回顾:(找学生回答)
提问:同学课下的复习很好。我们先来探讨这样一个问题:对于两个向量来说空间向量和平面向量有没有区别?
学生探讨研究:平面向量可在同一平面内平移,而空间向量也可在空间中平移。平移后的向量与原向量是同一向量。由此得出:空间任意两个向量都可转化为共面向量。
引导学生得出任意的空间中的两个向量的运算与平面向量的结论一致,这样我们就能够定义空间向量的加法和减法运算。
同样地,用类比(表格)形式对比给出空间向量的相关定义,采用填空形式填写下列有关内容:(课件)
(三)巩固提高
课堂练习例1.
(四)小结作业
这节课,我们在平面向量的基础上学习了平面向量,接下来给同学们两分钟的时间总结一下这节课的主要内容。(学生总结)
通过这节课的学习,我们学会了空间向量的有关概念,加减运算及其运算律以及空间向量的加减运算在空间几何体中的应用。
作业:(1)课后练习题1、2;
(2)思考题:共始点的两个不共线向量的加法满足平行四边形法则。和向量是平行四边形的对角线。请问,共始点的三个不共面的向量满足什么法则?和向量是什么向量?
【板书设计】
【答辩题目解析】
1.平行向量是如何定义的?
2.空间向量在高中数学中具有怎样的地位和作用?
考题
以下关于侧面安装装甲模块的说法中,所有的正确描述有() ①侧面装甲模块的支撑架底部连接面必须与XY平面平行,使得装甲模块受力面所在平面的法向量所在直线与Z轴负方向所在直线的锐角夹角为45° ②机器人侧面装甲模块不含指示灯的两条边与XY平面保持平行 ③机器人4块装甲模块的方向向量的单位向量必须分别等于机器人机体坐标系的正X轴、负X轴,正Y轴,负Y轴(方向向量和对应坐标轴向量之间的角度误差不能超过5°) ④机器人X,Y轴的装甲模块允许偏离几何中心正负50mmA、②③B、①②③④C、①②④D、②③④
考题
向量中断与非向量中断的区别在于()。A、非向量中断是单一中断源的中断,而向量中断是多中断源的中断B、非向量中断只有单一中断处理程序入口,而向量中断有多个中断处理程序入口C、非向量中断是单级中断,而向量中断可以实现多级中断D、非向量不能作为中断隐指令,而向量可以形成隐指令
考题
单选题向量中断与非向量中断的区别在于()。A
非向量中断是单一中断源的中断,而向量中断是多中断源的中断B
非向量中断只有单一中断处理程序入口,而向量中断有多个中断处理程序入口C
非向量中断是单级中断,而向量中断可以实现多级中断D
非向量不能作为中断隐指令,而向量可以形成隐指令
考题
单选题把平面上所有的单位向量归结到共同的始点,那么这些向量的终点所构成的图形是( ).A
一条线段B
一个圆面C
圆上的一群孤立点D
一个圆
热门标签
最新试卷