网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0. 8 X 10-3 Pa*s,在固壁处y = 0。距壁面y= 7. 5cm处的粘性切应力τ为:
A. 2X103Pa
B.-32X10-3Pa
C.1.48X10-3Pa
D.3.3X10-3Pa
B.-32X10-3Pa
C.1.48X10-3Pa
D.3.3X10-3Pa
参考答案
参考解析
解析: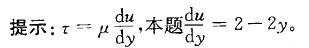
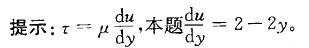
更多 “某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0. 8 X 10-3 Pa*s,在固壁处y = 0。距壁面y= 7. 5cm处的粘性切应力τ为: A. 2X103Pa B.-32X10-3Pa C.1.48X10-3Pa D.3.3X10-3Pa ” 相关考题
考题
黏度为 3.92*10-2Pa.s的黏性流体沿表面流动,距表面y处的流速为v=3*y+y2(m/s),则表面的切应力为()。
A. 5*10-3PaB. 11.76*10-3PaC. 11.76*10-2PaD. 11.76*10-4Pa
考题
一平面简谐波沿X轴正向传播,已知x=L(L<λ)处质点的振动方程为y=Acosωt,波速为u,那么x=0处质点的振动方程为( )。A.y=Acosω(t+L/u)
B.y=Acosω(t-L/u)
C.y=Acos(ωt+L/u)
D.y=Acos(ωt-L/u)
考题
—平面简谐波沿x轴正方向传播,振幅A=0. 02m,周期T=0. 5s,波长λ=100m,原点处质元的初相位φ=0,则波动方程的表达式为:
A.y=0.02cos2π(t/2-0.01x) (SI)
B.y=0.02cos2π(2t-0.01x) (SI)
C.y=0.02cos2π(t/2-100x) (SI)
D.y=0.02cos2π(2t-100x) (SI)
考题
一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI),则在t=0. 1s时刻,x=2m处质元的振动位移是:
A. 0. 01cm B. 0. 01m
C. -0. 01m D. 0. 01mm
考题
某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0. 8 X 10-3 Pa?s,在固壁处y = 0。距壁面y= 7. 5cm处的粘性切应力τ为:
A. 2X103Pa
B.-32X10-3Pa
C.1.48X10-3Pa
D.3.3X10-3Pa
考题
一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI),则在t=0. 1s时刻,x=2m处质元的振动位移是:
A. 0. 01cm
B. 0. 01m
C. -0. 01m
D. 0. 01mm
考题
已知曲面方程为x-yZ+z2-2x+8y+6z=10,则过点(5,-2.1)的切平面方程为( )。
A、2x+3y+2z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0
考题
已知某水流流速分布为μ=0.72y1/10,u的单位为m/s,y为距壁面的距离,单位为m。 (1)求y=0.1、0.5、1.0m处的流速梯度; (2)若水的运动粘滞系数ν=0.1010cm2/s,计算相应的切应力。
考题
一平面简谐波沿z轴正向传播,已知x=L(Lλ)处质点的振动方程为Y=Acoswt,波速为u,那么x=0处质点的振动方程为()。A、y=Acos(wt+L/u)B、y=Acos(wt-L/u)C、y=Acosw(t+L/u)D、y=Acosow(t-L/u)
考题
一平面简谐波沿X轴正向传播,已知x=L(Lλ)处质点的振动方程为y=Acos(∞t+φ0),波速为u,那么x=0处质点的振动方程为:()A、y=Acos[ω(t+L/u)+φ0]B、y=Acos[ω(t-L/u)+φ0]C、y=Acos[ωt+L/u+φ0]D、y=Acos[ωt-L/u+φ0]
考题
不可压缩流体平面流动在y方向的速度分量为uy=y2-2x+2y,根据连续性方程可知,速度在x方向的分量ux为()。A、-(2yx+2x)+f(y)B、2x(y+1)C、-(2yx+2y)+f(x)D、2x(y+1)+c
考题
一平面简谐波沿X轴正向传播,已知x=L(Lλ)处质点的振动方程为y=Acosωt,波速为u,那么x=0处质点的振动方程为()。A、y=Acosω(t+L/u)B、y=Acosω(t-L/u)C、y=Acos(ωt+L/u)D、y=Acos(ωt-L/u)
考题
单选题曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为( )。A
3(x-1)+2(y-2)=0B
4(x-1)+2(y-2)=0C
3(x-1)+(y-2)=0D
4(x-1)+(y-2)=0
考题
单选题某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0.8×10-3Pa·s,在固壁处y=0。距壁面y=7.5cm处的粘性切应力τ为()A
2×103PaB
-32×10-3PaC
1.48×10-3PaD
3.3×10-3Pa
考题
单选题曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为( )。A
4(x+1)+2(y-2)=0B
4(x-1)+2(y-2)=0C
4(x-1)-2(y-2)=0D
4(x-1)+2(y+2)=0
考题
单选题函数y=f(x)是由方程xy+2lnx=y4所确定,则曲线y=f(x)在点(1,1)处的切线方程为( )。A
x-y=0B
x+y=0C
-x-y=0D
-x+y=0
热门标签
最新试卷