网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
设X,Y相互独立,且X～N(1,2),Y～N(0,1),求2=2X－Y＋3的密度函数,

参考答案

参考解析
解析：【解】因为X，Y相互独立且都服从正态分布，所以X，Y的线性组合仍服从正态分布，即2=2X-Y+3服从正态分布，由E(Z)=2E(X)-E(Y)+3=5，D(Z)=4D(X)+D(Y)=9，则Z的密度函数为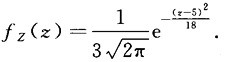
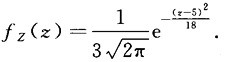
更多 “设X,Y相互独立,且X～N(1,2),Y～N(0,1),求2=2X－Y＋3的密度函数,” 相关考题
考题 设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X＋Y服从的分布为() A、X+Y服从N(0，1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布
查看答案
考题 设随机变量X和Y相互独立,且X~N(2,42),Y~N(3,92),则D(X＋Y)=()
查看答案
考题 设随机变量和是相互独立的随机变量且都服从正态分布,X~N(3,4),Y~N(2,9),求D(3X＋4Y)=()
查看答案
考题 假设X～N(-1,2),Y～N(1,3)，且X与Y相互独立，则X+2Y～A、N(1,8)B、N(1,14)C、N(1,40)D、N(1,22)
查看答案
考题 设随机变量X,Y相互独立,且X～N,Y～N,则与Z=Y-X同分布的随机变量是().A.X-Y B.X+Y C.X-2Y D.Y-2X
查看答案
考题 设随机变量X,Y相互独立,且X～N(0,1),Y～N(1,1),则().
查看答案
考题 设二维随机变量(X,Y)的联合密度函数为f(x,y)= 　　(1)求随机变量X,Y的边缘密度函数； 　　(2)判断随机变量X,Y是否相互独立； 　　(3)求随机变量Z=X+2Y的分布函数和密度函数.
查看答案
考题 设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相 　　关系数为－,又设Z= (1)求E(Z),D(Z)；(2)求；(3)X,Z是否相互独立？为什么？
查看答案
考题 设随机变量X,Y相互独立,且X～N,Y～N,Z=｜X-Y｜,求 　　E(Z),D(Z).
查看答案
考题 设X～N(0,1),y=X^2,求y的概率密度函数.
查看答案
考题 设随机变量X~U（0，1)，Y~E（1），且X,Y相互独立，求Z=X+Y的密度函数
查看答案
考题 设随机变量X～N(0,1),且y=9X^2,则y的密度函数为_______.
查看答案
考题 设随机变量X～U(0,1),Y～E(1),且X,Y相互独立,求随机变量Z=X+Y的概率密度.
查看答案
考题 设随机变量X～N(μ,σ^2),Y～U［－π,π］,X,Y相互独立,令Z=X+Y,求fz(z).
查看答案
考题 设随机变量X～U(0,1),在X=x(0　　(1)求X,y的联合密度函数； 　　(2)求y的边缘密度函数.
查看答案
考题 设X,Y相互独立,且X～B,Y～N(0,1),令U=max{X,Y},求P{1
查看答案
考题 设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.
查看答案
考题 设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求： 　　(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).
查看答案
考题 已知X-N（-3，1），Y-N（2，1），且X，Y相互独立，记Z=X-2Y+7则Z-（）.A、N（0，5）B、N（0，12）C、N（0，54）D、N（-1，2）
查看答案
考题 设X，Y是相互独立的随机变量，X~N（2，σ2），Y~N（-3，σ2），且P{|2X+Y-1|≤8.7654}=0.95，则σ=（）。
查看答案
考题 若随机变量X～N（－2，4），Y～N（3，9），且X与Y相互独立。设Z＝2X－Y＋5，则Z～（）。
查看答案
考题 若随机变量X～N（1，4），Y～N（2，9），且X与Y相互独立。设Z＝X－Y＋3，则Z～（）。
查看答案
考题 设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。
查看答案
考题 设随机变量X和Y相互独立，且X~N（0，1），Y~N（1，1），则（）A、P{X+Y≤0}=0.5B、P{X+Y≤1}=0.5C、P{X-Y≤0}=0.5D、P{X-Y≤1}=0.5
查看答案
考题 设随机变量X~N（-3，1），Y~N（2，1），且X，Y相互独立，记Z=X-2Y+7，则Z~（）。
查看答案
考题 设X，Y相互独立，且都服从标准正态分布N（0，1），令Z=X2+Y2则Z服从的分布是（）.A、N（0，2）分布B、单位圆上的均匀分布C、参数为1的瑞利分布D、N（0，1）分布
查看答案
考题 问答题设随机变景X与Y相互独立，且X服从[0,1]上的均匀分布，y服从λ=1的指数分布，　　求：(1)X与Y的联合分布函数.　　(2)X与y的联合概率密度函数.　　(3)P{X≥Y}.
查看答案
热门标签
最新试卷