网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。
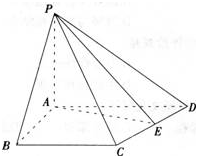
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。

参考答案
参考解析
解析:
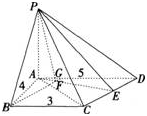
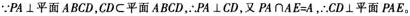



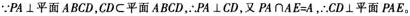

更多 “如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。 (1)证明:CD⊥平面PAE; (2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。 ” 相关考题
考题
在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
考题
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.
考题
如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。
A.12
B.14
C.15
D.16
考题
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。
考题
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。
A.1
B.2
C.3
D.4
考题
已知四棱锥P-ABCD底面为直角梯形,AB平行于DC,∠DAB=90°,PA垂直于底面ABCD,PA=AD=DC=
AB=1,M为PB中点。
(1)求证:面PAD⊥面PCD;
(2)求面AMC与面BMC所成二面角的余弦值。
考题
铰链四杆机构ABCD,如果以BC为机架(静件),当机构为双曲柄机构时,各杆的长度可为()。A、AB=130 BC=150 CD=175 AD=200B、AB=150 BC=130 CD=165 AD=200C、AB=175 BC=130 CD=185 AD=200D、AB=200 BC=150 CD=165 AD=130
考题
在下列铰链四杆机构中,若以BC杆件为机架,则能形成双摇杆机构的是()。 (1)AB=70mm,BC=60mm,CD=80mm,AD=95mm (2)AB=80mm,BC=85mm,CD=70mm,AD=55mm (3)AB=70mm,BC=60mm,CD=80mm,AD=85mm (4)AB=70mm,BC=85mm,CD=80mm,AD=60mmA、(1)、(2)、(4)B、(2)、(3)、(4)C、(1)、(2)、(3)
热门标签
最新试卷