网友您好, 请在下方输入框内输入要搜索的题目:
若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为______________ .
如图所示,点P为正方形ABCD内一点,且PA=1,PB=2,PC=3试求∠ABP的度数?
【题目描述】
如果点P(-1,b)在直线y=2x+3上,那么点P到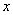 轴的距离为__________.
轴的距离为__________.
【参考答案分析】:
1

(1)求证:BE是⊙0的切线;
(2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。
∵AO=BO,∴∠BAD=∠ABO,
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°,
∵B0是圆的半径,∴BE是⊙O的切线。
(2)设圆的半径为r,连接CD交OB于F,

设圆的半径为R,连接CD,.

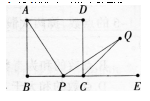

∴AP=PQ。
摘要:八年级数学第十一十二章解答题1、已知:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等。(不写作法,保留作图痕迹)2、如图,在△ABC中,AD,AE分别是边BC上的中线和高,(1)若AE=3cm,S△ABC=12cm2.求DC的长.(2)若∠C-∠B=300,求∠DAE的大小.3、在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠EAF=180°,求证DE=DF.4.如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.(1)求∠E的度数.(2)请猜想∠A与∠E之间的数量关系,请说明理由. 5.(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.6.如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中

(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。

(1)若点P(-1,0)在f(x)的图象上,过点P的切线与直线y=-x+2平行,求f(x)的解析式;
(2)若f(x)在区间[0,2]上单调递增,求b的取值范围。

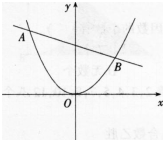
(1)直线ι经过一个定点C,试求出点C的坐标;(2分)
(2)若m=-1,已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合),且△ABP的面积为(3√13)/2,求点P的坐标。(6分)


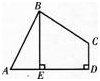
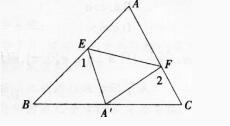
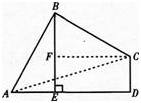
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
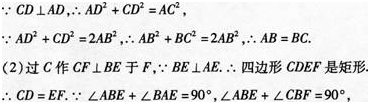

更多 “人教版数学八年级上册第十一十二章测试题(含答案)” 相关考题
- 预聚物收率控制在()gPE/mMTi。A、35~45B、20~30C、30~50D、40~60
- 多选题针对重大和特别重大事故的隐患,企业应该建立预警机制,按隐患危害程度分()四级预警。A红色B橙色C黄色D绿色E蓝色
- 单选题()不得转包或者违法分包工程。A 施工单位B 建设单位C 房地产公司D 所有建筑相关部门
- 单选题总承包单位和分包单位就分包工程对建设单位()。A 独立承担各自的责任B 承担过错的责任C 承担适当的责任D 承担连带责任
- 填空题()年,美国社会学鼻祖()在芝加哥大学创建了社会学系。
- 影响精馏塔正常采出的因素有()。A、LV634阀故障B、冷却器失去作用C、F620罐压高于塔压D、F690罐压高于塔压
- 在要求小流量、高压力的输液系统,应选用()。A、离心泵B、往复泵C、齿轮泵D、真空泵
- 判断题腐败是经济发展的润滑剂,腐败是有益处的。A 对B 错
- 多选题管理系统由三种动力,即()。A物质动力B精神动力C信息动力D外部压力
- D200操作温度是()℃。A、68±2B、68±5C、70±2D、70±5