网友您好， 请在下方输入框内输入要搜索的题目：
请你写出一个有一根为1的一元二次方程：____________．
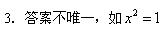
如果2是一元二次方程x2＋bx＋2＝0的一个根，那么常数b的值为________________．
-3
请结合自己的看法简要谈一下一元二次方程根的判别式在中学数学中的重要性。
纲要：(1)一元二次方程根的判别式的公式；
(2)举例说明一元二次方程根的判别式的应用：①判断一元二次方程(或二元二次方程组)的根的情况；或已知根的情况，求方程(或组)中的待定系数的取值范围；②判断二次三项式在实数范围内是否能进行因式分解；③判断二次函数的图像与x轴有无交点，或已知交点情况，确定待定系数的值。
打开考生文件夹下的DB数据库，完成如下简单应用： 1．编写一个名为FOUR．PRG的程序，根据表TABA中所有记录的a，b，c三个字段的值，计算各记录的一元二次方程的两个根x1和x2，并将两个根x1和x2写到对应的字段x1和x2中，如果无实数解，在note字段中写入“无实数解”。提示：平方根函数为SQRT；程序编写完成后，运行该程序计算一元二次方程的两个根。注意：一元二次方程公式如下：
2．打开名为testA的表单，其中有两个命令按钮，界面要求如下： (1)设置两个按钮的高度均为30，宽度均为80，“退出”按钮与“查询”按钮顶边对齐。 (2)“查询”按钮的功能是在该按钮的Click事件中使用SQL的SELECT命令从表TABA中查询“无实数解”的记录并存储到表TABD中。 (3)“退出”按钮的功能是关闭并释放表单。 请按要求完成表单的设计，表单设计完成后，运行该表单，并单击“查询”按钮进行查询。
(1)【操作步骤】
新建程序four，并输入以下命令：
*******”four”程序文件中的代码*******CLOSALL
USETABASCAN
IFA<>0ANDB*B一4*A*C>=0
REPLx1WITH(-B+SQRT(B*B一4*A*C))/(2*A)，x2WITH(-B-SQRT(B*B一4*A*C))/(2*A)
ELSE
REPLNOTEWITH”无实数解”ENDIF
ENDSCAN****************************
最后保存运行程序。
(2)【操作步骤】
步骤1：打开表单“testA”。
步骤2：按Shift的同时选中“查询”和“退出”两个按钮，然后在属性窗口设定它们的Height属性为30，Width属性为80，在系统菜单中选择“格式”→“对齐”→“顶边对齐”。
步骤3：在“查询”按钮的Click事件中输入下列代码。
*******”three”程序文件中的代码*******
SELECT*；FROMTABA；WHERETABA．note=”无实数解”；
INTOTABLETABD．dbf
****************************
步骤4：在“退出”命令按钮的Click事件中输入“This．
Form．Release”。保存并运行表单。
一元二次方程x2+x-2=0 的两根之积是（ ）
A．-1
B．-2
C．1
D．2
1.1一元二次方程自主学习优生提升训练1关于x的一元二次方程x2+kx20的一个根为1，则k的值为（）A1B1C2D22已知x1是一元二次方程（m2）x2+4xm20的一个根，则m的值为（）A1或2B1C2D03已知m是一元二次方程x2x30的根，则代数式2m22m+7的值是（）A11B12C13D144已知M2x22x+1，Nax2+bx+c（a，b，c为常数），若存在x使得MN，则a，b，c的值可以分别为（）A1，1，0B1，0，1C0，1，1D0，1，15若m是方程x2x10的一个根，则m2m+2020的值为（）A2019B2020C2021D20226将方程（x1）26化成一元二次方程的一般形式，正确的是（）Ax22x+50Bx22x50Cx2+2x50Dx2+2x+507若x2是一元二次方程x23x+a0的一个根，则a的值是（）A0B1C2D38我们知道方程x2+2x30的解是x11，x23，现给出另一个方程（2x1）2+2（2x130，它的解是（）Ax11，x2-3Bx1-1，x23Cx11，x23Dx11，x219若方程（m1）xm2+1（m+1）x20是关于x的一元二次方程，则m的值为（）A0B1C1D110若关于x的方程x2+mx3n0的一个根是3，则mn的值是（）A1B3C1D311关于x的一元二次方程（a1）x2+x+a210的一个根是0，则a的值是（）A1B1C1或1D1或012若x23x+10，则x4+的个位数字是（）A7B8C9D1013已知是方程x23x+c0的一个根，则c的值是（）A6B6CD214若方程（m1）x2+x+0是关于x的一元二次方程，则下列结论正确的是（）Am2Bm2Cm2且m1Dm115若a22a20，则（a1）2 16已知a是方程x2+3x40的根，则代数式2a2+6a+4的值是 17关于x的方程a（x+m）2+b0的解是x12，x21，（a，m，b均为常数，a0），则方程a（x+m+2）2+b0的解是 18已知ABC的两边长分别为2和3，第三边长是方程（x22x）5（x2）0的根，求ABC的周长19若a是方程x22020x+10的一个根，求代数式a22021a+的值20已知x0是关于x的一元二次方程（m1）x2+mx+4m240的一个根，求直线ymx2经过哪些象限答案1解：把x1代入方程x2+kx20，可得12+k20，即k1，故选：A2解：把x1代入（m2）x2+4xm20得：m2+4m20，m2+m+20，解得：m12，m21，（m2）x2+4xm20是一元二次方程，m20，m2，m1，故选：B3解：m是一元二次方程x2x30的根，m2m30，m2m3，2m22m+72（m2m）+723+713故选：C4解：由M2x22x+1，Nax2+bx+c（a，b，c为常数），且MN，得到2x22x+1ax2+bx+c，即（a2）x2+（b+2）x+c10，则a，b，c的值可以分别为0，1，1，即2x2+x0，方程有解，故选：D5解：m是方程x2x10的一个根，m2m10，m2m1，m2m+20201+20202021故选：C6解：（x1）26，x22x+160，x22x50，即将方程（x1）26化成一般形式为x22x50，故选：B7解：把x2代入方程x23x+a0得46+a0，解得a2故选：C8解：把方程（2x-1）2+2（2x-1）30看作关于2x-1的一元二次方程，所以2x-11或2x-13，所以x11，x21故选：D9解：由题意得：m2+12，m10，解得m1，故选：D10解：依题意得：32+3m3n0，整理，得9+3（mn）0解得mn3故选：B11解：关于x的一元二次方程（a1）x2+x+a210的一个根是0，（a1）0+0+a210，且a10，解得a1且a1a1符合题意；故选：A12解：依题意得，当x0时不符合题意，故x0，由原方程得到：x+3，x2+7x4+（x2+）2249247则x4+的个位数字是7故选：A13解：把x代入方程x23x+c0得：39+c0，解得：c6，故选：B14解：（m1）x2+x+0是关于x的一元二次方程，m10，解得m1，故选：D15解：a22a20，a22a2，（a1）2a22a+12+13故316解：a是方程x2+3x40的根，a2+3a40，a2+3a4，2a2+6a+42（a2+3a）+424+412故1217解：关于x的方程a（x+m）2+b0的解是x12，x21，（a，m，b均为常数，a0），方程a（x+m+2）2+b0变形为a（x+2）+m2+b0，即此方程中x+22或x+21，解得x4或x1故x34，x4118解：解方程（x22x）5（x2）0可得x2或x5，ABC的第三边为2或5，但当第三边为5时，2+35，不满足三角形三边关系，ABC的第三边长为2，ABC的周长为2+2+3719解：a是方程x22020x+10的一个根，a22020a+10，a22020a1，a22021a+2020a12021a+a+a1120解：x0是关于x的一元二次方程（m1）x2+mx+4m240的一个根，4m240，解得：m1，根据题意，得m10，m1，m10直线ymx2经过的象限是第二、三、四象限
B.χ2+χ-11=0
C.χ2-11χ-1=0
D.χ2+χ+1=0
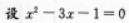的两根分别为χ1，χ2，则由根与系数的关系得χ1+χ2=3，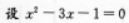
又所求方程的两根为
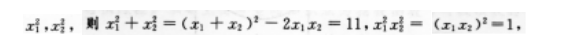
∴所求方程为χ2-11χ+1=0．
B.x2-10x+64=0
C.x2-20x+8=0
D.x2-20x+64=0
一、考题回顾
【教学过程】
(一)引入新课
复习回顾一元二次方程的一般形式以及求根公式。
提出问题：一元二次方程的根与方程中的系数之间有怎样的关系呢?
引出课题。
(四)小结作业
提问：今天有什么收获?引导学生回顾：一元二次方程根与系数的关系以及推导证明过程。
作业：课后练习。
【板书设计】
【答辩题目解析】
1.教学目标是什么?
【参考答案】
(1)知识与技能
学生知道一元二次方程根与系数的关系，并会应用根与系数关系解决问题。
(2)过程与方法
学生能够借助问题的引导，发现、归纳并证明一元二次方程根与系数的关系，在探究过程中，感受由特殊到一般地认识事物的规律。
(3)情感态度价值观
通过探索一元二次方程的根与系数的关系，激发发现规律的积极性，鼓励勇于探索的精神。
一、考题回顾
二、考题解析
【教学过程】
(一)引入新课
复习旧知：回顾之前学习过哪些方程，并对一元一次方程的定义进行回顾。
总结：明确本节课学习初中阶段的最后一种方程，《一元二次方程》。
【板书设计】
【答辩题目解析】
1.谈一谈你本节课导入的设计意图是什么?
2.一元二次方程、二次函数、一元二次不等式之间的联系是什么?
这样的设计既可以考察学生对之前知识的掌握情况，还能够为今天学习一元二次方程的概念打下基础。
2、三者之间联系非常的紧密：一元二次方程的根为二次函数与x轴交点的横坐标;一元二次不等式的解集其中大于0的部分为二次函数在x轴上方函数图象的定义域，小于0部分为二次函数在x轴下方函数图象的定义域。
【教师甲】
设置问题：请同学们根据下列问题，只列出含未知数的方程：
预设：学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排序，右侧为零的形式，然后引导学生完成下面两件事：对比“一元一次方程”的定义，为这类方程定义一个名称——一元二次方程。再请学生自行写出几个不同的一元二次方程，并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问：什么是“一元一次方程”？请你根据“一元一次方程”的定义，给出“一元二次方程”的定义，并举出几个“一元二次方程”的例子。在学生举例的基础上，提炼出“一元二次方程”的一般表达式。
请完成下列任务：
（1）请分析两位老师引入“一元二次方程”概念设计方案的各自的特点。（15分）
（2）在教学中，当引入一个新的数学概念之后，往往通过例题、习题加深对概念的理解。请针对“一元二次方程”概念，设计不同难度的两道例题和两道练习题，加深学生对“一元二次方程”概念的理解。（15分）
（1）教学活动是师生积极参与、交往互动、共同发展的过程。有效的教学活动是学生学与教师教的统一，学生是学习的主体，教师是学习的组织者、引导者和合作者。数学教学活动应激发学生的学习兴趣，调动学生积极性，引发学生思考，鼓励学生的创造性思维。在教学的过程中教师应培养学生良好的数学学习习惯，使学生掌握恰当的数学学习方法。也注重以学生的认知发展水平和已有经验为基础，面向全体学生，采取启发式和因材施教的教学。学生在生动活泼的、主动的教学课堂中，更容易吸收知识，但也应注重多种学习方式相结合，除接受学习外，动手实践、主动探索与合作交流同样是学习数学的重要方式。
教师甲的教学方案，相对于乙教师来说，更加非常符合素质教育的要求。
（2）针对“一元二次方程”概念，设计不同难度的两道例题和两道练习题，题目的难度应适当，目的是加深学生对“一元二次方程”概念的理解。
更多 “20212022学年苏科版九年级数学上册《1.1一元二次方程》自主学习优生提升训练【含答案】” 相关考题
- 有时候我们的行为是受（ ）控制的，因而这类行为通常是暂时性、非普遍性的，不属于个体稳定的人格特征。A.情境B.基因C.情绪D.兴趣
- 几何公差带形状是距离为公差值t的两平行平面内区域的有()
- ( 难度：中等)Hive与传统关系型数据库对比，优势有A.计算能力更强B.延迟更低C.扩展性更好D.索引各类更多
- 马汉认为海军是什么性质的军种？
- 本行为收款行，他行为付款行，这类凭证又称为代付票据.
- 抵押贷款是保证贷款的一种常见的银行贷款。
- 关于人格与性格，下面说法错误的是（ ）A.人格比性格更多地受环境影响B.性格带有正面或负面的明显社会评价色彩C.性格是人格中涉及社会评价的那部分内容D.性格指的是人的一惯的和稳定的心理特征、思维和行为方式
- 贷款损失准备的计提,不论是本币资产还是外币资产，必须以人民币计提。
- Response对象的（）方法可以将缓冲区中的页面内容立即输出到客户端。A. WriteB. EndC. ClearD. Flush
- 金融行业的所有资产都是金融资产。