网友您好， 请在下方输入框内输入要搜索的题目：
此题为判断题(对，错)。
应用计算机求解管网计算问题时应用最广的一种方法是（ ）。
A．解管段方程
B．解节点方程
C．解环方程
D．解流量方程
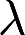取何值时,非齐次线性方程组
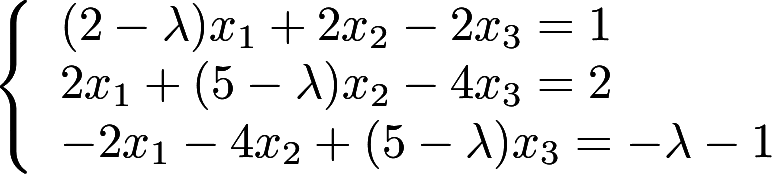(1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时，求方程组的通解。
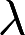取何值时 非齐次线性方程组
， (1)有唯一解 (2)无解 (3)有无穷多个解，并在无穷多个解时，求方程组的通解
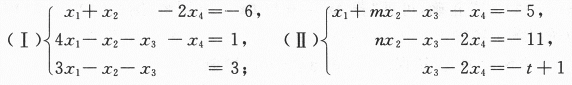
(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解.
(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.
4.5解简易方程练习题及答案 篇一：五年级数学解简易方程测(五)附 （人教版）数学上册 解简易方程 一、填空 （1）使方程左右两边相等的_，叫做方程。 （2）被减数=差（ ）减数，除数=（ ）（ ） （3）求_的过程叫做解方程。 （4）小明买5支钢笔，每支a元；买4支铅笔，每支b元。一共付出（ ）元。 二、判断 1.含有未知数的式子叫做方程。（ ） 2. 3. 、 都是方程。（ ） 的解是 =3。（ ） 4.等式不一定是方程，方程一定是等式。（ ） 三、选择 1.下面的式子中，（ ）是方程。 153=12 6 1=6 79 2.方程9.5 =9.5的解是（ ） =9.+5 =19 =0 3. =3.7是下面方程（）的解。 6 9=15 3 =4.5 18.8 =4 四、解方程 52 =15 91 =1.3 =3 五、用方程表示下面的数量关系，并求出方程的解1. 的3倍等于8.4 2.7除 等于0.9 3. 减42.6的差是3.4。 参考答案 一、（1）未知数的值（2）；被除数商 （3）方程的解 （4）5A4B 二、（1）（2）（3）（4） 三、（1）（2）（3） 四、 =37 = =2.4 =0.2 五、1解： =8.4 =8.43 =2.8 2解： 7=0.9 6.3 3. 解： 42.6=3.4 42.63.4 46 篇二：五年级上册数学解简易方程习题及答案 五年级上册数学解简易方程习题及答案（人教版） 一、填空 （1）使方程左右两边相等的_，叫做方程。 （2）被减数=差（ ）减数，除数=（ ）（ ） （3）求_的过程叫做解方程。 （4）小明买5支钢笔，每支a元；买4支铅笔，每支b元。一共付出（ ）元。 二、判断 1.含有未知数的式子叫做方程。（ ） 2.4x+5、6x=8 都是方程。（ ） 3.18x=6的解是x=3。（ ） 4.等式不一定是方程，方程一定是等式。（ ） 三、选择 1.下面的式子中，（ ）是方程。 25x 153=12 6x 1=6 4x79 2.方程9.5x =9.5的解是（ ） x=9.5 x=19 x=0 3. x=3.7是下面方程（ ）的解。 6x9=15 3x=4.5 18.8x=4 四、解方程 52x=15 91x=1.3 x+8.3=10.7 15x=3 五、用方程表示下面的数量关系，并求出方程的解 1. x的3倍等于8.4 2. 7除x等于0.9 3. x减42.6的差是3.4 篇三：五年级上册数学解简易方程练习题整单元 解简易方程习题（一） 一、细心填一填 1方程 2x6x4.8 的解是_；x_是方程 155x15的解。 2有三个连续自然数，如果中间一个用 表示，那么其他两个可用_和_表示。 3已知白兔有x只，黑兔的只数是白兔的4倍。黑兔有_只，黑兔和白兔一共有_只。 4一辆汽车每小时行48千米，t小时行_千米，行s千米需要_小时。 5两个数的和是252，甲数是乙数的8倍，甲数是_，乙数是_。 6李老师到体育商店买了4个篮球共花去a元，又买了一个足球花去b元，那么一个足球比一个篮球便宜_元。 7师傅每小时生产x个零件，徒弟每小时生产y个零件，他们一天工作8个小时。 (1)师傅每天生产零件_个。 (2)徒弟和师傅两人一天共生产零件_个。 (3)师傅每小时比徒弟多生产零件_个。 (4)两人工作一天，徒弟比师傅少生产零件_个。 二、慧眼辨一辨 1 x8是方程 4x537的解。（ ） 2有些应用题，我们既可以用方程解，也可以用算术方法解。（ ） 3方程一定是等式，等式也一定是方程。（ ） 4方程3x+3=27与方程2x+2=18的解相同。（ ） 5含有未知数的式子叫做方程。（ ） 6 4x5、 6x8都是方程。（ ） 7 18x6的解是 x3。（ ） 三、仔细选一选 1a与b的和的4倍，用式子表示是（ ）。 Aa+4b B4a+b C4（a+b） 2小英今年11岁，比小军小a岁，3年后小军（ ）岁。 A14-a B17+a C14+a 3已知a人4天修路1600米，求a人1天修路多少米的算式是（ ）。 A1600a4 B16004 C1600a 4等腰三角形的一条腰长4厘米，底长为x厘米，它的周长为（ ）厘米。 A 8x B 2x4C (x4)2 四、耐心算一算 14x2.18.5 2 8x5.7x69 31.240.8x2.5 4 (97.6)x6.764.8 五、列方程并求解 1一个数的一半减去3.8等于22，求这个数。 2一个数的4倍比它的7倍少9.6，求这个数。 35.6加上 x的4倍，等于12.8，求x。 4一个数的4.5倍减去1.2与5的积，差是7.5，求这个数。 5一个数的5倍加上1.5与4.6的积，和是24.4。求这个数。 解下列方程 2(x2.6)8 5(x1.5)17.5 8(x6.2)41.6 (x3)27.5 一、开心填空。 1甲数比乙数少5，设乙数是x，甲数是（ ），甲乙两数的和是（）。 2一本书有a页，小敏每天看b页，看了c天后，还剩（ ）页。 3一个长方形的长是a米，宽是3米，它的周长是（ ）米，面积是（）平方米。 4乘法分配律用字母表示是（ ）。 5爸爸今年m岁，比儿子大n岁，mn表示（）。 6如果3x+6=24，那么5x7=（）。 7五（1）班有女生x人，比男生少5人，男生有（）人，全班有（ ）人。 8有三个连续的自然数，第一个是b，第二个是（ ），第三个是（）。 9一辆汽车t小时行了s千米，每小时行（）千米； 行100千米要（）小时 。 二、辨别真假。（对的打“”，错的打“”） 1所有的等式都是方程。 （） 2x=3是方程 8+2 x =30的解。 ( ) 3小数0.3535是纯循环小数。 ( ) 4因为22=22，所以x2=x2。 （） 5方程53.2=3 x与5=3 x3.2的解是相同的。 （） 三、慧眼识金。（将正确答案的序号填在括号里） 1含有（ ）的等式叫方程。 A字母 B未知数C等号 2下列各式中不是方程的
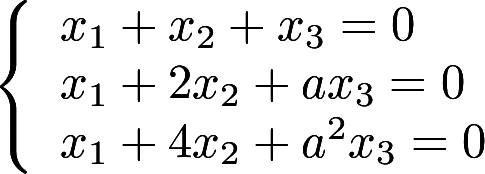与方
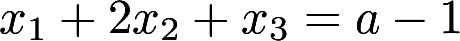程有公共解，求a的值及所有公共解
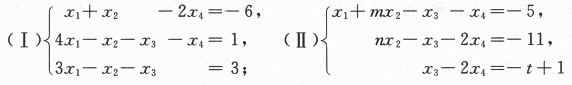
(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解.
(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.
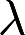取何值时,非齐次线性方程组
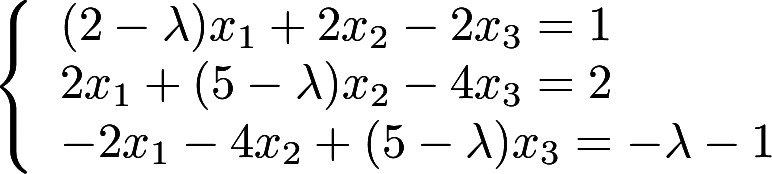(1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时，求方程组的通解。
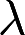取何值时 非齐次线性方程组
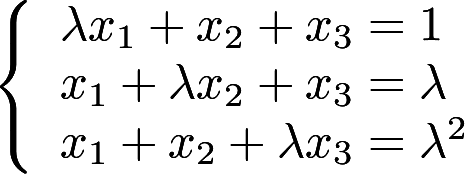， (1)有唯一解 (2)无解 (3)有无穷多个解，并在无穷多个解时，求方程组的通解
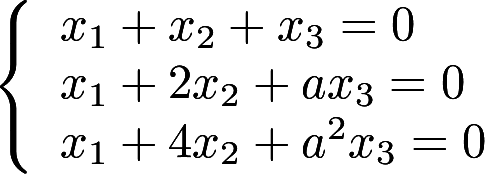与方
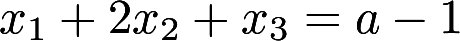程有公共解，求a的值及所有公共解
更多 “4.5解简易方程练习题及答案” 相关考题
- 单选题移动方案中，基站接入PTN960设备的PW在汇聚核心PTN6900-X8上终结，并采用PW-APS保护，PW分别接入（）汇聚核心PTN6900-X8设备？A 1个B 2个C 3个D 4个
- 用于方便残疾旅客出入座位有以下特征（）A、靠过道一侧的座椅扶手可以往上翻起B、椅背可以向后但不能向前放倒C、椅背可以向前但不能向后放倒D、整个座椅可以向前翻起
- 单选题为了防止DCN网络过大引起网元负荷过重，导致网络隐患，建议对DCN网络进行区域划分，每个网关网元带的非网关网元不超过（）个。A 64B 128C 256D 512
- 母液不来结晶的原因及处理方法？
- 泵的正常流量应不小于额定流量的一半。
- 试分析中国内地与香港发展经贸关系的重要意义。
- 对外贸易社会经济效益
- 乘坐公司国内航班的旅客可以携带的非托运行李体积不得超过（）A、25*45*56CMB、20*40*50CMC、20*40*55CMD、30*40*55CM
- 属于1979—1992年我国对外贸易管理的特点的是（）A、管理措施比较完整B、管理的法规、条例、制度比较健全C、管理措施逐步向规范化法制化发展D、计划管理与行政命令是管理的主要手段
- 水上迫降撤离后，鞋子应（）还给旅客。A、立即B、所有人上船后C、到达陆地后D、旅客情绪稳定后