网友您好， 请在下方输入框内输入要搜索的题目：

苏教版初中数学八年级下第二学期第14周周考试卷

若反比例函数的图象经过点A(-2,1) ,则它的表达式是 _________________ ．


正确答案：

作出函数y=3-2x的图象，根据图象回答下列问题：

（1）y的值随着x值增大而__________;

（2）图象与x轴的交点坐标是_________________，

与y轴的交点坐标是_______________；

（3）当x__________时，y＞0 。

在同一直角坐标系内一次作出函数y=x+1，y=2x+1，y=3x+1的图象。

（1）这几个图象之间有什么差别，又有什么联系？

（2）一次函数y=kx+b的一次项系数k对函数的图象有什么影响？


（1）这几个图像都经过（0,1）点，且y都随x的增大而增大，但是这几个图像的倾斜程度不同。

（2）对图像倾斜度有影响！


你认为作反比例函数图象时应注意哪些问题？


列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;

列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;

连线时一定要养成按自变量从小到大的顺序，依次用平滑的曲线连接,从中体会函数的增减性；


已知函数 y=x²-4x+3。

（1）画出函数的图象；

（2）观察图象，当x取哪些值时，函数值为0？

苏教版初中数学八年级下册第二学期第14周周考试卷班级 姓名 得分 一、选择题（每小题3分，共30分）1、反比例函数y图象经过点（2，3），则n的值是（）A、2 B、1 C、0 D、12、若反比例函数y（k0）的图象经过点（1，2），则这个函数的图象一定经过点（）A、（2，1） B、（，2） C、（2，1） D、（，2）3、已知甲、乙两地相距（km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间（h）与行驶速度（km/h）的函数关系图象大致是（ ）t/hv/(km/h)Ot/hv/(km/h)Ot/hv/(km/h)Ot/hv/(km/h)OABCD4、若y与x成正比例，x与z成反比例，则y与z之间的关系是（）A、成正比例 B、成反比例 C、不成正比例也不成反比例 D、无法确定5、一次函数ykxk，y随x的增大而减小，那么反比例函数y满足（）A、当x0时，y0B、在每个象限内，y随x的增大而减小C、图象分布在第一、三象限 D、图象分布在第二、四象限6、如图，点P是x轴正半轴上一个动点，过点P作x轴的垂线PQ交双曲线y于点Q，连结OQ，点P沿x轴正方向运动时，RtQOP的面积（）A、逐渐增大B、逐渐减小C、保持不变D、无法确定7、在一个可以改变容积的密闭容器内，装有一定质量m的某种气体，当改变容积V时，气体的密度也随之改变与V在一定范围内满足，它的图象如图所示，则该气体的质量m为（）A、1.4kgB、5kgC、6.4kgD、7kg8、若A（3，y1），B（2，y2），C（1，y3）三点都在函数y的图象上，则y1，y2，y3的大小关系是（）A、y1y2y3B、y1y2y3C、y1y2y3D、y1y3y29、已知反比例函数y的图象上有A（x1，y1）、B（x2，y2）两点，当x1x20时，y1y2，则m的取值范围是（）A、m0B、m0C、mD、m10、如图，一次函数与反比例函数的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（）A、x1B、x2C、1x0或x2D、x1或0x2二、填空题（每小题4分，共28分）11.某种灯的使用寿命为1000小时，它的可使用天数与平均每天使用的小时数之间的函数关系式为 . 12、已知反比例函数的图象分布在第二、四象限，则在一次函数中，随的增大而 （填“增大”或“减小”或“不变” ）13、若反比例函数y和一次函数y3xb的图象有两个交点，且有一个交点的纵坐标为6，则b 14、反比例函数y（m2）xm10的图象分布在第二、四象限内，则m的值为 15、有一面积为S的梯形，其上底是下底长的，若下底长为x，高为y，则y与x的函数关系是 16、如图，点M是反比例函数y（a0）的图象上一点，过M点作x轴、y轴的平行线，若S阴影5，则此反比例函数解析式为 17、过双曲线y（k0）上任意一点引x轴和y轴的垂线，所得长方形的面积为_三、解答题（共42分）18、（6分）如图，P是反比例函数图象上的一点，且点P到x轴的距离为3，到y轴的距离为2，求这个反比例函数的解析式19、（8分）如图，已知A（x1，y1），B（x2，y2）是双曲线y在第一象限内的分支上的两点，连结OA、OB（1）试说明y1OAy1；（2）过B作BCx轴于C，当k4时，求BOC的面积20、（8分）如图，已知反比例函数y与一次函数ykxb的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是2求：（1）一次函数的解析式；（2）AOB的面积21、（8分）如图，一次函数yaxb的图象与反比例函数y的图象交于M、N两点（1）求反比例函数与一次函数的解析式；（2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围22、（12分）如图， 已知反比例函数y的图象与一次函数yaxb的图象交于M（2，m）和N（1，4）两点（1） 求这两个函数的解析式；（2） 求MON的面积；（3）请判断点P（4，1）是否在这个反比例函数的图象上，并说明理由

画出函数 y=x²-2x-3的图象，利用图象回答：

（1）方程 x²-2x-3=0 的解是什么；

（2）x取什么值时，函数值大于0 ；

（3）x取什么值时，函数值小于0 。

命题p:不经过第一象限的图象所对应的函数一定不是幂函数.命题q:函数y=x+2/x的单调递增区间是[-√2,0)∪[√2,+∞), 则下列命题中,真命题是( ).

(A)p∧q.

(B)(￢p)∨q.

(C)(￢p)∧(￢q).

(D)p∧(￢q).


参考答案D

已知函数f(x)=a2+k的图象经过点(1，7)，且其反函数f-1(x)的图像经过点(4，0)，则函数f(x)的表达式是 （ ）

A．f(x)=4x+3

B．f(x)=2x+5

C．f(x)=5x+2

D．f(x)=3x+5


正确答案：A

请教:2012年初中数学《函数及其图象》测验卷第2大题第1小题如何解答?

【题目描述】

如果点P（－1,b）在直线y=2x+3上，那么点P到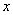轴的距离为__________.

 


【参考答案分析】：

1

请教:2012年初中数学《函数及其图象》测验卷第1大题第1小题如何解答?

【题目描述】

函数y=的自变量的取值范围是( )

A、x>0且x≠0

B、x≥0且x≠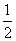

C、x≥0

D、x≠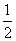

 

 


正确答案：B

更多 “苏教版初中数学八年级下第二学期第14周周考试卷” 相关考题
考题 定义[a，b，c]为函数y=ax2+bc+c的特征数，下面给出特征数为[ 2m ，1-m，-1-m]的函数的一些结论： ①当m=-3时，函数图象的顶点坐标是{1/3,-(8/3)}； ②当m>0时，函数图象截石轴所得的线段长度大于3/2； ③当m1/4时，y随x的增大而减小； ④当m≠0时，函数图象经过同一个点。 其中正确的结论有()。 A.②③④ B.①②④ C.③④ D.②④ 答案：D解析：特征数[2m，1-m，-l-m]的函数为y=2mx2+(1-m)x+(-1-m)。①当m=-3时，y=-6x2+4x+
查看答案
考题 将1、2、3三个数字随机生成的点的坐标，列成下表。如果每个点出现的可能性相等，那么从中任意取一点，则这个点在函数y=x图象上的概率是 （1，1）（1，2）（1，3）（2，1）（2，2）（2，3）（3，1）（3，2）（3，3）A．0．3 B．0．5 C．1/3 D2/3 正确答案：C
查看答案
考题 关于反比例函数y=2/x，下列说法不正确的是()。，A.点(-2，-1)在它的图象上 B.它的图象在第一、三象限 C.当x>0时，y随x增大而增大 D.当x答案：C解析：当x>0时，y随x增大而减小。
查看答案
考题 三次函数y=aχ3+bχ2+cχ+d的导函数图象如图l． 则此三次函数的图象是( )。 答案：B解析：若f（x）在某个区间I内有导数，则f（x）≥0，(x∈I)f（x）在I内为增函数：f’(x)≤O，x∈If（x）在I内为减函数。结合图I中导函数的函数值从左到右依次大于0、小于0、大于0，因此原函数图 象从左到右变化趋势依次是单调递增、单调递减、单调递增。因此选B。
查看答案
考题 若函数f(x)的图象上点P(1，m)处的切线方程为3x-y+b=0，则m的值为__________。 答案：解析：
查看答案
考题 下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)． (1)求出图象与戈轴的交点A，B的坐标； 存在，请说明理由； ° (3)将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b(b＜1)与此图象有两个公共点时，b的取值范围． 答案：解析：解：(1)由二次函数Y=(x+m)2+k的顶点坐标为M(1，-4)可知，m=-1，k=-4.则二次函数Y=(x-1)2-4与x轴的交点为A(-1，0)，8(3，0). (3)如图，当直线Y=x+b经过A(-1，0)时-1+b=0， 可得b=1，又因为b＜1， 故可知Y=x+b在Y=x+1的下方， 当直线Y=x+b经过点B(3，0)时，3+b=0，则b=-3， 由图可知，b的取值范围为-3＜b＜1时， 直线Y=x+b(b＜1)与此图象有两个公共点.
查看答案
考题 单选题如果一个正比例函数的图象经过不同象限的两点A（2，m），B（n，３），那么一定有（　　）．A m＞0，n＞0B m＞0，n＜0C m＜0，n＞0D m＜0，n＜0正确答案： B 解析： 因为A，B是不同象限的点，而正比例函数的图象要不在一、三象限或在二、四象限，由点A与点B的横纵坐标可以知：点A与点B在一、三象限时：横纵坐标的符号应一致，显然此题不可能，点A与点B在二、四象限：点A在四象限得m＜0，点B在二象限得n＜0．(另解：就有两种情况一、三或二、四象限，代入特值即可判定)
查看答案
考题 若一次函数y=ax+b的图象经过第二、三、四象限，则下列不等式总是能成立的是()。A.abB.a-b>0 C.|a|-|b|>0 D.a+b答案：D解析：一次函数y=ax+b的图象经过第二、三、四象限，则一定有a0，a-b与|a|-|b|个式子与0的大小关系无法确定。
查看答案
考题 单选题如果一个正比例函数的图象经过不同象限的两点A（2，m），B（n，３），那么一定有（　　）．A m＞0，n＞0B m＞0，n＜0C m＜0，n＞0D m＜0，n＜0正确答案： B 解析： 因为A，B是不同象限的点，而正比例函数的图象要不在一、三象限或在二、四象限，由点A与点B的横纵坐标可以知：点A与点B在一、三象限时：横纵坐标的符号应一致，显然此题不可能，点A与点B在二、四象限：点A在四象限得m＜0，点B在二象限得n＜0．(另解：就有两种情况一、三或二、四象限，代入特值即可判定)
查看答案
考题 案例： 某教师关于“反比例函数图象”教学过程中的三个步骤为： 第一步：复习回顾 提出问题：我们已经学过一次函数的哪些内容 是如何研究的 第二步：引入新课。 提出问题：反比例函数的图象是什么形状呢 引导学生利用描点法画出y=1/2的图象。 列表： 描点： 连线：引导学生用光滑的曲线连接描点，并用计算机演示图象的生成过程。在此过程中启发学生思考，由于X，Y都不能为0，所以函数图象与X轴、Y轴不能有交点(如下图) ……(第三步过程省略) (1)该教学过程的主要特点是什么 (8分) (2)在第二步的连线过程中，如果你是该老师，如何引导学生思考所连的线不是直线，而是光滑曲线(6分) (3)对于第三步的③，如果你是该老师，如何引导学生思考函数图象在第一象限(或第三象限)的变化 (6分) 答案：解析：(1)在导入过程运用了温故知新导人，优势是可以帮助学生复习已经学习过的知识，从学习过的知识当中找到前后联系。从而引出新课题，帮助学生快速进入课堂。 在新课教学过程中让学生通过动手操作画出反比例函数图象，但是在引导学生运用列表法的时候选出的点不够有代表性，x轴不能都是整数，可以随机的选取一部分分数，为下边讲解函数图象是一条光滑的曲线做准备。 另外在此过程中利用现代教学手段，计算机演示是一种很好的教学方法，可以很直观的将函数图象的动态画面展示给学生．方便学生建立数形结合的意识。 第三步．组织学生观察讨论曲线特点，根据选取图象中若干特殊点，总结在第一象限以及第三象限的变化情况。 (2)反比例函数图象的特点是光滑的曲线，而不是折线，这是区别一次函数图象最大的特点，首先我会请学生分小组讨论这个问题。如果反函数的图象的点是用折线连起来会是什么图形，用曲线连起来会是什么图形。给学生3分钟时间讨论，在讨论的过程中我会给与学生提示，我们选取的点是有限的，其实反比例函数的点是无数个的．为什么正多边形的边无限增多就变成了光滑的圆。讨论结束有小组代表回答，鉴于这个问题有难度，在学生回答结束之后我会给予详细的讲解：反比例函数的图象可通过描点法给出，折线是由若干直线组合而成，而直线必须对应一个一次函数，显然反比例函数不能对应到一次函数上，所以它不是折线，而是曲线。另外我们只是描了图象上少数的几个点，图象构架比较空，所以自然地认为看起来应该用折线连，如果多描几个点，多到密密麻麻的情况．就会明白其实这个就和“正多边形边数越多越接近圆。圆就是正多边形边数无限大时的情况”的道理是一样的。逐步提升学生有限无限思想。 (3)在此环节我将组织学生通过选取若干特殊点进行比较，独立思索曲线的变化情况，并鼓励学生大胆说出自己的想法，并给予鼓励，已达到锻炼学生从数学模型中抽象出数学结论的能力，对于数学图象的变化得到初步的锻炼以及提升。
查看答案
热门标签
最新考题
最新试卷
热门试卷